题目内容
【题目】在△ABC中,A=![]() ,
, ![]() =
=![]() .
.
(Ⅰ)试求tanC的值;
(Ⅱ)若a=5,试求△ABC的面积.
【答案】(Ⅰ)tanC=![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由正弦定理得: ![]() ,将A=
,将A=![]() 代入求解得4sinC=3cosC,进而得tanC的值;
代入求解得4sinC=3cosC,进而得tanC的值;
(Ⅱ)结合条件由余弦定理a2=b2+c2-2bccosA得25=b2+(![]() b)2-2b×
b)2-2b×![]() b×
b×![]() .求解b,c代入S=
.求解b,c代入S=![]() bcsinA求解面积即可.
bcsinA求解面积即可.
试题解析:
(Ⅰ)因为A=![]() ,
, ![]() =
=![]() ,所以
,所以![]() =
= =
=![]() .
.
所以7sinC=3![]()
所以7sinC=3![]()
所以7sinC=3cosC+3sinC.
所以4sinC=3cosC.
所以tanC=![]() .
.
(Ⅱ)因为A=![]() ,
, ![]() =
=![]() ,a=5,由余弦定理a2=b2+c2-2bccosA得25=b2+(
,a=5,由余弦定理a2=b2+c2-2bccosA得25=b2+(![]() b)2-2b×
b)2-2b×![]() b×
b×![]() .
.
所以b=7,c=3![]() .
.
所以△ABC的面积S=![]() bcsinA=
bcsinA=![]() ×7×3
×7×3![]() ×
×![]() .
.

【题目】已知椭圆![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,若点
,若点![]() 总在以线段
总在以线段![]() 为直径的圆内,求
为直径的圆内,求![]() 的取值范围.
的取值范围.
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
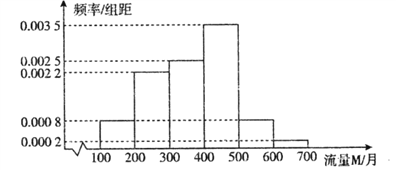
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
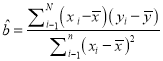 ,
, ![]()
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
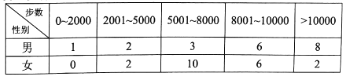
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 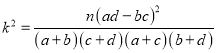 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.