题目内容

【题目】已知函数f（x）=log （3x2﹣ax+5）在[﹣1，+∞）上单调递减，则实数a的取值范围是（ ）
A.[﹣8，﹣6]
B.（﹣8，﹣6]
C.（﹣∞，﹣8）∪（﹣6，+∞）
D.（﹣∞，﹣6]

【答案】B
【解析】解：设t=g（x）=3x2﹣ax+5，则函数y=log t在定义域上为减函数，
∵函数f（x）=log （3x2﹣ax+5）在[﹣1，+∞）上单调递减，
∴t=g（x）=3x2﹣ax+5在[﹣1，+∞）上单调递增，且满足g（﹣1）＞0，
即 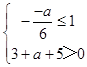，得 ，即﹣8＜a≤﹣6，
故选：B．
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识，掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”．

练习册系列答案
相关题目

【题目】已知f（x）是定义在[﹣1，1]上的奇函数，当x∈[﹣1，0]时，函数的解析式为f（x）= ﹣ （a∈R）．
（1）求出f（x）在[0，1]上的解析式；
（2）求f（x）在[﹣1，0]上的最大值．
（3）对任意的x1 ， x2∈[﹣1，1]都有|f（x1）﹣f（x2）|≤M成立，求最小的整数M的值．

【题目】已知函数f（x）= x2﹣alnx+ （a∈R） （Ⅰ）求函数f（x）单调区间；
（Ⅱ）若a=﹣1，求证：当x＞1时，f（x）＜ x3 ．

【题目】若点P在椭圆 +y2=1上，F1、F2分别是椭圆的两焦点，且∠F1PF2=60°，则△F1PF2的面积是（ ）
A.
B.
C.
D.

【题目】在英国的某一娱乐节目中，有一种过关游戏，规则如下：转动图中转盘（一个圆盘四等分，在每块区域内分别标有数字1,2,3,4），由转盘停止时指针所指数字决定是否过关.在闯关时，转次，当次转得数字之和大于时，算闯关成功，并继续闯关，否则停止闯关，闯过第一关能获得10欧元，之后每多闯一关，奖金翻倍，假设每个参与者都会持续闯关到不能过关为止，并且转盘每次转出结果相互独立.

（1）求某人参加一次游戏，恰好获得10欧元的概率；

（2）某人参加一次游戏，获得奖金欧元，求的概率分布和数学期望.

【题目】如图，三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，AC=BC= AA1 ， D是棱AA1的中点，DC1⊥BD．
（1）证明：DC1⊥面BCD；
（2）设AA1=2，求点B1到平面BDC1的距离．

【题目】对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，给出定义：设f′(x)是函数y＝f(x)的导数，f″(x)是f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．某同学经过探究发现：任何一个三次函数都有对称中心，且“拐点”就是对称中心．若，请你根据这一发现判断函数的对称中心为(　　)

A. (，1) B. (－，1) C. (，－1) D. (－，－1)

【题目】（本小题满分10分）选修4-5：不等式选讲

已知函数f（x）=log2（|x+1|+|x﹣2|﹣m）．

（1）当m=7时，求函数f（x）的定义域；

（2）若关于x的不等式f（x）≥2的解集是R，求m的取值范围．

【题目】下列函数是偶函数的是（ ）
A.y=1﹣lg|x|
B.
C.
D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网