题目内容
【题目】在数列{an}中,设ai=2m(i∈N* , 3m﹣2≤i<3m+1,m∈N*),Si=ai+ai+3+ai+6+ai+9+ai+12 , 则满足Si∈[1000,3000]的i的值为 .
【答案】2
【解析】解:∵3m﹣2≤i<3m+1,
∴3(m+1)﹣2≤i+3<3(m+1)+1,
∴ai+3=2m+1 ,
同理可得:ai+6=2m+2 , ai+9=2m+3 , ai+12=2m+4 .
∴Si=2m+2m+1+2m+2+2m+3+2m+4=(1+2+4+8+16)2m=312m .
∴1000≤312m≤3000.
∴ ![]() ≤2m≤
≤2m≤ ![]() ,
,
∵m∈N* , ∴2m=64.∴m=6.
∵3×2﹣2≤6<3×2+1,
∴i=2.
所以答案是:2.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系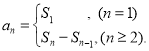 .
.

 名校课堂系列答案
名校课堂系列答案【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.