题目内容
【题目】设直线4x﹣3y+12=0的倾斜角为A
（1）求tan2A的值；
（2）求cos（ 
﹣A）的值．
【答案】
（1）解：由4x﹣3y+12=0，
得：k= 
，则tanA= ，
∴tan2A= 
=﹣ 
（2）解：由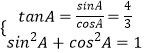 
，以及0＜A＜π，
得：sinA= 
，cosA= 
，
cos（ 
﹣A）=cos cosA+sin sinA= 
× + 
× = 
【解析】（1）求出tanA，根据二倍角公式，求出tan2A的值即可；（2）根据同角的三角函数的关系分别求出sinA和cosA，代入两角差的余弦公式计算即可．
【考点精析】认真审题，首先需要了解两角和与差的余弦公式(两角和与差的余弦公式：
)，还要掌握直线的倾斜角(当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°)的相关知识才是答题的关键．
练习册系列答案
阅读快车系列答案
相关题目
【题目】【2017湖南娄底二模】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如下表：
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：
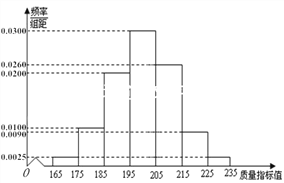
（Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定？
（Ⅱ）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（Ⅲ）该企业为提高产品质量，开展了“质量提升月”活动，活动后在抽样检测，产品质量指标值
近似满足
，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？