题目内容
已知点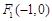 ,
,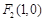 ,动点G满足
,动点G满足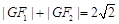 .
.
(Ⅰ)求动点G的轨迹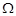 的方程;
的方程;
(Ⅱ)已知过点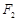 且与
且与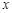 轴不垂直的直线l交(Ⅰ)中的轨迹
轴不垂直的直线l交(Ⅰ)中的轨迹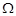 于P,Q两点.在线段
于P,Q两点.在线段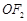 上是否存在点
上是否存在点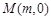 ,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
(Ⅰ)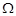 的方程是
的方程是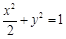 .(Ⅱ)存在,实数m的取值范围是
.(Ⅱ)存在,实数m的取值范围是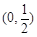 .
.
解析试题分析:(Ⅰ)由椭圆的定义知,动点G的轨迹是以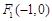 ,
,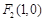 为焦点的椭圆,由题设即可得动点G的轨迹
为焦点的椭圆,由题设即可得动点G的轨迹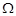 的方程.(Ⅱ)要使得以MP、MQ为邻边的平行四边形是菱形,只需
的方程.(Ⅱ)要使得以MP、MQ为邻边的平行四边形是菱形,只需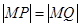 即可.设
即可.设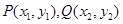 ,则
,则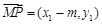 ,
,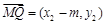 ,由
,由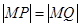 得
得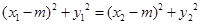 移项用平方差公式得
移项用平方差公式得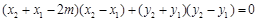 ①
①
设直线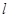 的方程为
的方程为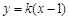
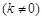 ,则
,则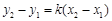 ,
,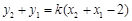 ,故①式变形为
,故①式变形为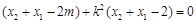 ,然后用韦达定理可得一个
,然后用韦达定理可得一个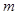 与
与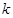 的关系式:
的关系式: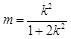
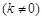 ,由此关系式可看出,这样的点
,由此关系式可看出,这样的点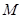 存在,并由
存在,并由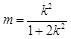 可求出
可求出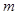 的取值范围.
的取值范围.
另外,由于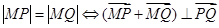 ,所以也可利用
,所以也可利用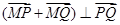 得:
得: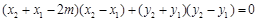 .
.
试题解析:(Ⅰ)由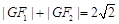 ,且
,且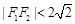 知,动点G的轨迹是以
知,动点G的轨迹是以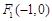 ,
,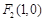 为焦点的椭圆,设该椭圆的标准方程为
为焦点的椭圆,设该椭圆的标准方程为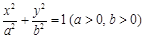 ,
,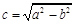 ,
,
由题知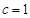 ,
,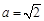 ,则
,则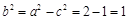 ,
,
故动点G的轨迹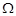 的方程是
的方程是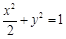 . 4分
. 4分
(Ⅱ)假设在线段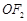 上存在
上存在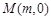
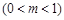 ,使得以MP、MQ为邻边的平行四边形是菱形.直线l与
,使得以MP、MQ为邻边的平行四边形是菱形.直线l与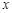 轴不垂直,设直线
轴不垂直,设直线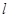 的方程为
的方程为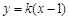
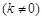 ,
,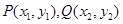 ,
,
由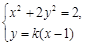 可得
可得 .
.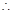
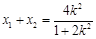 ,
, 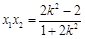 . 6分
. 6分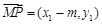 ,
,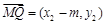 ,
,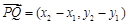 ,其中
,其中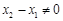 .
.
由于MP,MQ为邻边的平行四边形是菱形,
所以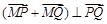 ,则有
,则有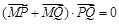 , 8分
, 8分
从而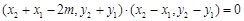 ,
,
所以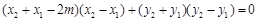 ,
,
又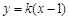 ,则
,则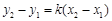 ,
,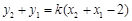 ,
,
故上式变形为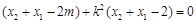 , 10分
, 10分
将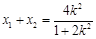 代入上式,得
代入上式,得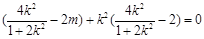 ,
,
即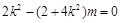 ,所以
,所以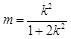
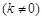 ,可知
,可知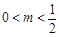 .
.
故实数m的取值范围是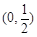 . ..13分
. ..13分
考点:1、椭圆的方程;2、直线与圆锥曲线的关系.

练习册系列答案
相关题目
 的顶在坐标原点,焦点
的顶在坐标原点,焦点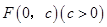 到直线
到直线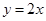 的距离是
的距离是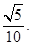
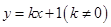 与抛物线
与抛物线 两点,设线段
两点,设线段 的中垂线与
的中垂线与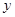 轴交于点
轴交于点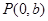 ,求
,求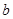 的取值范围.
的取值范围. 的左、右焦点分别为
的左、右焦点分别为 、
、 ,
, 为原点.
为原点.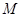 为椭圆
为椭圆 上的一点,
上的一点,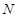 是
是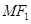 的中点,且
的中点,且 ,求点
,求点 轴的距离;
轴的距离;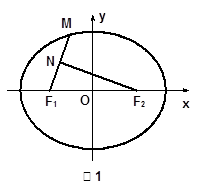
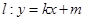 与椭圆
与椭圆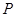 、
、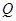 两点,若在椭圆
两点,若在椭圆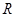 ,使四边形
,使四边形 为平行四边形,求
为平行四边形,求 的取值范围.
的取值范围.
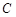 :
: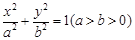 的离心率为
的离心率为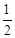 ,右焦点为
,右焦点为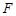 ,右顶点
,右顶点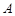 在圆
在圆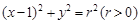 上.
上. 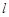 与椭圆
与椭圆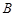 ,与圆
,与圆 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线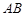 的中点,若存在,求出直线
的中点,若存在,求出直线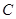 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长为
轴上,长轴长为 ,且点
,且点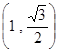 在椭圆
在椭圆 是椭圆
是椭圆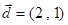 的直线
的直线 交椭圆
交椭圆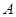 、
、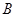 两点,求证:
两点,求证: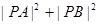 为定值.
为定值.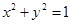 上一个动点,M为点P在y轴上的投影,动点Q满足
上一个动点,M为点P在y轴上的投影,动点Q满足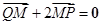 .
.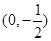 ,交曲线C于A、B两点,且A、B同在以点D(0,1)为圆心的圆上,求直线l的方程。
,交曲线C于A、B两点,且A、B同在以点D(0,1)为圆心的圆上,求直线l的方程。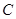 的离心率
的离心率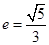 ,一条准线方程为
,一条准线方程为
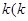 >0)为斜率的直线
>0)为斜率的直线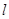 与椭圆
与椭圆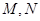 ,且线段
,且线段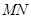 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为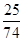 ,求
,求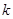 的取值范围。
的取值范围。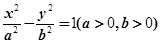 ,
,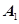 、
、 是双曲线的左右顶点,
是双曲线的左右顶点,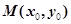 是双曲线上除两顶点外的一点,直线
是双曲线上除两顶点外的一点,直线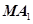 与直线
与直线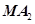 的斜率之积是
的斜率之积是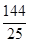 ,
,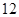 ,求双曲线的方程.
,求双曲线的方程.