题目内容
已知抛物线 的顶在坐标原点,焦点
的顶在坐标原点,焦点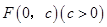 到直线
到直线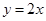 的距离是
的距离是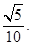
(1)求抛物线 的方程;
的方程;
(2)若直线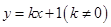 与抛物线
与抛物线 交于
交于 两点,设线段
两点,设线段 的中垂线与
的中垂线与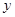 轴交于点
轴交于点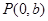 ,求
,求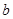 的取值范围.
的取值范围.
(1)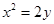 (2)
(2)
解析试题分析:(1)已知点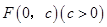 到直线
到直线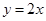 的距离利用距离公式
的距离利用距离公式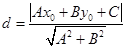 可求得
可求得 ,可直接写出抛物线方程; (2)把直线方程与抛物线方程联立整理成二次方程
,可直接写出抛物线方程; (2)把直线方程与抛物线方程联立整理成二次方程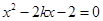 ,用韦达定理可求出线段
,用韦达定理可求出线段 中点的坐标
中点的坐标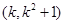 ,再写出中垂线方程
,再写出中垂线方程 ,即可求出直线与
,即可求出直线与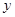 轴交点的纵坐标
轴交点的纵坐标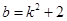 ,利用二次函数求值域的方法可求出
,利用二次函数求值域的方法可求出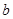 的范围.这个过程中不用讨论判别式,不用讨论斜率,值域也是二次函数的值域问题,是直线与圆锥曲线中的较易者.
的范围.这个过程中不用讨论判别式,不用讨论斜率,值域也是二次函数的值域问题,是直线与圆锥曲线中的较易者.
试题解析:(1)由题意,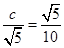 ,故
,故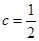
所以抛物线 的方程为
的方程为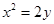 .
.
(2)设 ,则由
,则由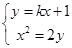 得
得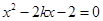 ,
,
则 ,所以线段
,所以线段 的中点坐标为
的中点坐标为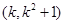 ,
,
线段 的中垂线方程为
的中垂线方程为 ,
,
即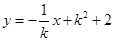 ,令
,令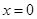 ,则
,则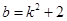 ,
,
所以 .
.
考点:直线与抛物线的位置关系.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
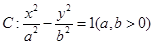 的一条渐近线方程是
的一条渐近线方程是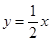 ,它的一个焦点在抛物线
,它的一个焦点在抛物线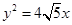 的准线上,点
的准线上,点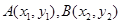 是双曲线
是双曲线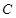 右支上相异两点,且满足
右支上相异两点,且满足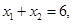
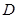 为线段
为线段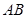 的中点,直线
的中点,直线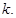
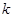 表示点
表示点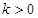 ,
, 轴于点
轴于点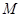 ,直线
,直线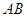 交
交 ,求
,求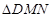 的面积的取值范围.
的面积的取值范围. 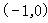 ,且离心率
,且离心率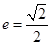 的椭圆
的椭圆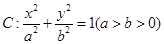 上下两顶点分别为
上下两顶点分别为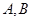 ,直线
,直线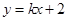 交椭圆
交椭圆 于
于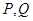 两点,直线
两点,直线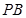 与直线
与直线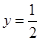 交于点
交于点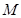 .
.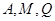 三点共线.
三点共线. 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为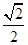 ,P是椭圆上一点,且
,P是椭圆上一点,且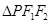 面积的最大值等于2.
面积的最大值等于2.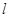 与直线
与直线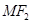 垂直,试判断直线
垂直,试判断直线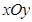 中,已知点
中,已知点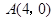 ,动点
,动点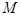 在
在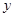 轴上的正射影为点
轴上的正射影为点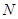 ,且满足直线
,且满足直线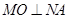 .
. 时,求直线
时,求直线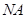 的方程.
的方程.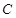 :
: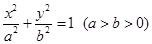 的左、右焦点分别为
的左、右焦点分别为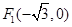 、
、 ,椭圆上的点
,椭圆上的点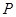 满足
满足 ,且△
,且△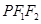 的面积为
的面积为 .
.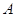 、
、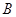 ,过点
,过点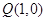 的动直线
的动直线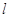 与椭圆
与椭圆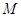 、
、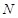 两点,直线
两点,直线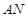 与直线
与直线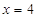 的交点为
的交点为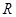 ,证明:点
,证明:点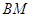 上.
上.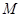 :
: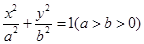 经过点
经过点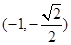 ,
,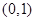 .
.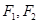 ,过点
,过点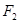 的直线交椭圆
的直线交椭圆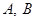 两点,求
两点,求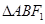 面积的最大值.
面积的最大值.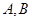 是抛物线
是抛物线 上的两个点,点
上的两个点,点 的坐标为
的坐标为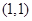 ,直线
,直线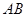 的斜率为
的斜率为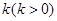 .设抛物线
.设抛物线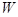 的焦点在直线
的焦点在直线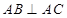 ,过
,过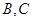 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为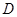 . 判断四边形
. 判断四边形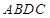 是否为梯形,并说明理由.
是否为梯形,并说明理由.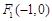 ,
,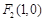 ,动点G满足
,动点G满足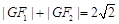 .
.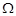 的方程;
的方程;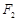 且与
且与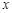 轴不垂直的直线l交(Ⅰ)中的轨迹
轴不垂直的直线l交(Ⅰ)中的轨迹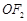 上是否存在点
上是否存在点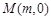 ,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.