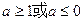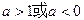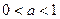题目内容
(本题满分14分) 设函数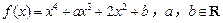 .
.
(Ⅰ)当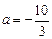 时,讨论函数
时,讨论函数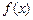 的单调性;
的单调性;
(Ⅱ)若函数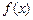 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;
(Ⅲ)若对于任何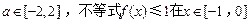 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
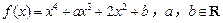 .
.(Ⅰ)当
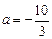 时,讨论函数
时,讨论函数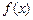 的单调性;
的单调性;(Ⅱ)若函数
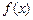 仅在x=0处有极值,试求a的取值范围;
仅在x=0处有极值,试求a的取值范围;(Ⅲ)若对于任何
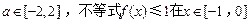 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.(1)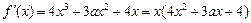 ,
,
当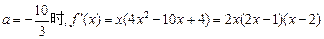
令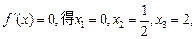
当x变化时,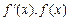 的变化情况如下表:
的变化情况如下表:
所以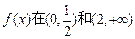 上是增函数,
上是增函数,
在区间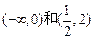 上是减函数;…………………………(4分)
上是减函数;…………………………(4分)
(2)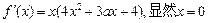 不是方程
不是方程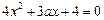 的根,
的根,
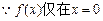 处有极值。
处有极值。
则方程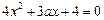 有两个相等的实根或无实根,
有两个相等的实根或无实根,
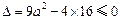 ,
,
解此不等式,得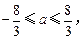
这时,f(0)=b是唯一极值,
因此满足条件的a的取值范围是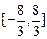 ;……………………(8分)
;……………………(8分)
注:若未考虑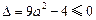 ,进而得到a的范围为
,进而得到a的范围为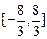 ,扣2分,
,扣2分,
(3)由(2)知,当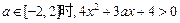 恒成立,
恒成立,
当x<0时,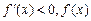 在区间
在区间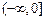 上是减函数,
上是减函数,
因此函数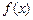 在[-1,0]上最大值是f(-1), …………(10分)
在[-1,0]上最大值是f(-1), …………(10分)
又∵对任意的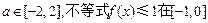 上恒成立,
上恒成立,
∴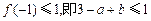 ,
,
于是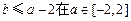 上恒成立。
上恒成立。
∴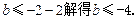
因此满足条件的b的取值范围是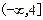 . …………………………(14分)
. …………………………(14分)
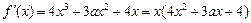 ,
,当
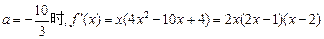
令
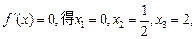
当x变化时,
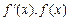 的变化情况如下表:
的变化情况如下表:| x | 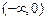 | 0 | 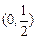 | 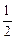 | 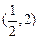 | 0 | 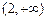 |
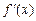 | - | 0 | + | 0 | - | 0 | + |
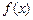 | 单调 递减 | 极小值 | 单调 递增 | 极大值 | 单调 递减 | 极小值 | 单调 递增 |
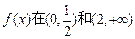 上是增函数,
上是增函数,在区间
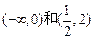 上是减函数;…………………………(4分)
上是减函数;…………………………(4分)(2)
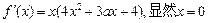 不是方程
不是方程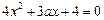 的根,
的根,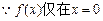 处有极值。
处有极值。则方程
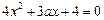 有两个相等的实根或无实根,
有两个相等的实根或无实根,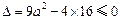 ,
,解此不等式,得
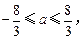
这时,f(0)=b是唯一极值,
因此满足条件的a的取值范围是
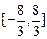 ;……………………(8分)
;……………………(8分)注:若未考虑
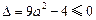 ,进而得到a的范围为
,进而得到a的范围为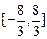 ,扣2分,
,扣2分,(3)由(2)知,当
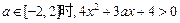 恒成立,
恒成立,当x<0时,
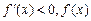 在区间
在区间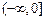 上是减函数,
上是减函数,因此函数
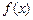 在[-1,0]上最大值是f(-1), …………(10分)
在[-1,0]上最大值是f(-1), …………(10分)又∵对任意的
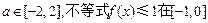 上恒成立,
上恒成立,∴
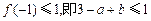 ,
,于是
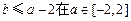 上恒成立。
上恒成立。∴
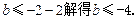
因此满足条件的b的取值范围是
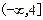 . …………………………(14分)
. …………………………(14分)略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
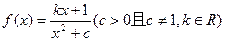 恰有一个极大值点和一个极小值点,其中的一个极值点是
恰有一个极大值点和一个极小值点,其中的一个极值点是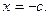
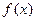 的另一个极值点;
的另一个极值点;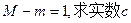 的值.
的值.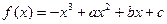 图象上的点
图象上的点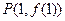 处的切线方程为
处的切线方程为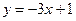 。若函数
。若函数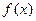 在
在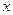 =-2处有极值,求
=-2处有极值,求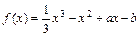 ,
,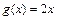 ,当
,当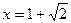 时,
时,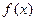 取得极值。
取得极值。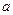 的值;
的值;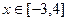 时,函数
时,函数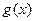 的图象有三个公共点,求
的图象有三个公共点,求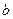 的取值范围。
的取值范围。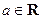 ,若函数
,若函数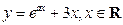 有大于零的极值点,则
有大于零的极值点,则



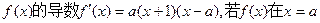 处取到极大值
处取到极大值 ,则a的取值范围是 .
,则a的取值范围是 .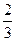 与
与 x=1时都取得极值.
x=1时都取得极值. 。
。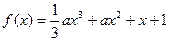 有极值的充要条件是 ( )
有极值的充要条件是 ( )