Question

【题目】在△ABC中，已知BC边上的高所在直线的方程为x﹣2y+1=0，∠A平分线所在直线的方程为y=0，若点B的坐标为（1，2）， （Ⅰ）求直线BC的方程；
（Ⅱ）求点C的坐标．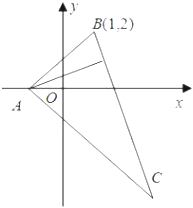

Answer 1

【答案】解：（Ⅰ）设BC边上的高为AD， ∵BC与AD互相垂直，且AD的斜率为 ，
∴直线BC的斜率为k= =﹣2，
结合B（1，2），可得BC的点斜式方程：y﹣2=﹣2（x﹣1），
化简整理，得 2x+y﹣4=0，即为所求的直线BC方程．
（Ⅱ）由x﹣2y+1=0和y=0联解，得A（﹣1，0）
由此可得直线AB方程为： ，即y=x+1
∵AB，AC关于角A平分线x轴对称，
∴直线AC的方程为：y=﹣x﹣1
∵直线BC方程为y=﹣2x+4
∴将AC、BC方程联解，得x=5，y=﹣6
因此，可得C点的坐标为（5，﹣6）．

【解析】（I）根据垂直的位置关系，算出直线BC的斜率为﹣2，利用直线方程的点斜式列式，化简整理即可得到直线BC的方程；（II）由BC边的高所在直线方程和y=0，解出A（﹣1，0），从而得出直线AB的方程．由直线AC、AB关于直线y=0对称，算出AC方程，最后将AC方程与BC方程联解，即可得出点C的坐标．
【考点精析】本题主要考查了一般式方程的相关知识点，需要掌握直线的一般式方程：关于的二元一次方程（A，B不同时为0）才能正确解答此题．