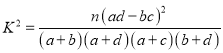题目内容
【题目】若直线 ![]() 与直线2x+3y﹣6=0的交点位于第一象限,则直线l的倾斜角的取值范围( )
与直线2x+3y﹣6=0的交点位于第一象限,则直线l的倾斜角的取值范围( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:联立两直线方程得: ![]() , 将①代入②得:x=
, 将①代入②得:x= ![]() ③,把③代入①,求得y=
③,把③代入①,求得y= ![]() ,
,
所以两直线的交点坐标为( ![]() ,
, ![]() ),
),
因为两直线的交点在第一象限,所以得到 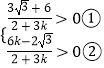 ,
,
由①解得:k>﹣ ![]() ;由②解得k>
;由②解得k> ![]() 或k<﹣
或k<﹣ ![]() ,所以不等式的解集为:k>
,所以不等式的解集为:k> ![]() ,
,
设直线l的倾斜角为θ,则tanθ> ![]() ,所以θ∈(
,所以θ∈( ![]() ,
, ![]() ).
).
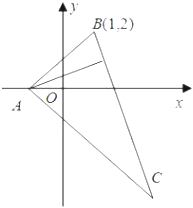
方法二、∵直线l恒过定点(0,﹣ ![]() ),作出两直线的图象.,
),作出两直线的图象.,
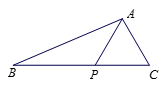
设直线2x+3y﹣6=0与x轴交于点A,与y轴交于点B.从图中看出,
斜率kAP<k<+∞,即 ![]() <k<+∞,
<k<+∞,
故直线l的倾斜角的取值范围应为( ![]() ,
, ![]() ).
).
故选B.
联立两直线方程到底一个二元一次方程组,求出方程组的解集即可得到交点的坐标,根据交点在第一象限得到横纵坐标都大于0,联立得到关于k的不等式组,求出不等式组的解集即可得到k的范围,然后根据直线的倾斜角的正切值等于斜率k,根据正切函数图象得到倾斜角的范围.

 口算题卡北京妇女儿童出版社系列答案
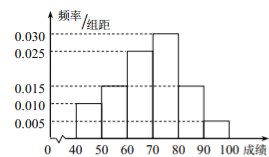
口算题卡北京妇女儿童出版社系列答案【题目】近年来,我国电子商务蓬勃发展. 2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的![]() 列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:![]()
![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |