题目内容
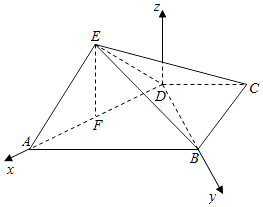
【题目】如图,四棱锥E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2. 
(1)求证:BD⊥平面ADE;
(2)求直线BE和平面CDE所成角的正弦值.
【答案】
(1)证明:∵EA=ED=2,EA⊥ED,∴AD=2 ![]() .
.
∵BC=CD=2,BC⊥CD,∴BD=2 ![]()
又AB=4,∴AD2+BD2=AB2,∴AD⊥BD.
又平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD,BD平面ABCD,
∴BD⊥平面ADE
(2)解:取AD的中点F,连接EF,则EF⊥平面ABCD,EF= ![]() .
.
过D点作直线Oz∥EF,则Oz⊥平面ABCD.
以D为坐标原点,以DA,DB,Dz为坐标轴建立空间直角坐标系D﹣xyz,
∴D(0,0,0),C(﹣ ![]() ,
, ![]() ,0),B(0,2
,0),B(0,2 ![]() ,0),E(
,0),E( ![]() ,0,
,0, ![]() ),
),
∴ ![]() =(
=( ![]() ,﹣2
,﹣2 ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0).
,0).
设平面CDE的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则 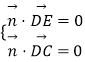 ,
,
∴ ![]() ,设x=1得
,设x=1得 ![]() =(1,1,﹣1).
=(1,1,﹣1).
∴cos< ![]() >=
>= ![]() =
= ![]() =﹣
=﹣
∴直线BE和平面CDE所成角的正弦值为 ![]() .
.
【解析】(1)由勾股定理得出AD=BD=2 ![]() ,故而AD⊥BD,由面面垂直的性质得出BD⊥平面ADE;(2)以D为原点建立坐标系,求出
,故而AD⊥BD,由面面垂直的性质得出BD⊥平面ADE;(2)以D为原点建立坐标系,求出 ![]() 和平面CDE的法向量
和平面CDE的法向量 ![]() ,则直线BE和平面CDE所成角的正弦值为|cos<
,则直线BE和平面CDE所成角的正弦值为|cos< ![]() >|.
>|.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则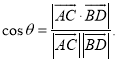 .
.

【题目】乡大学生携手回乡创业,他们引进某种果树在家乡进行种植试验.他们分别在五种不同的试验田中种植了这种果树100株并记录了五种不同的试验田中果树的死亡数,得到如下数据:
试验田 | 试验田1 | 试验田2 | 试验田3 | 试验田4 | 试验田5 |
死亡数 | 23 | 32 | 24 | 29 | 17 |
(Ⅰ)求这五种不同的试验田中果树的平均死亡数;
(Ⅱ)从五种不同的试验田中随机取两种试验田的果树死亡数,记为x,y,用(x,y)的形式列出所有的基本事件,其中(x,y)和(y,x)视为同一事件,并求![]() 的概率.
的概率.
【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图,把该直方图所得频率估计为概率.
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校2017年6月7、8、9日将作为高考考场,若这三天中某天出现5级重度污染,需要净化空气费用10000元,出现6级严重污染,需要净化空气费用20000元,记这三天净化空气总费用为X元,求X的分布列及数学期望.
【题目】某商场为了解该商场某商品近5年日销售量(单位:件),随机抽取近5年50天的销售量,统计结果如下:
日销售量 | 100 | 150 |
天数 | 30 | 20 |
频率 |
|
|
若将上表中频率视为概率,且每天的销售量相互独立.则在这5年中:
(1)求5天中恰好有3天销售量为150件的概率(用分式表示);
(2)已知每件该商品的利润为20元,用X表示该商品某两天销售的利润和(单位: 元),求X的分布列和数学期望.

