题目内容
【题目】如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=t,建立如图所示的空间直角坐标系O—xyz.
(1)若t=1,求异面直线AC1与A1B所成角的大小;
(2)若t=5,求直线AC1与平面A1BD所成角的正弦值;
(3)若二面角A1—BD—C的大小为120°,求实数t的值.

【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(1)先根据坐标表示向量![]() ,
,![]() ,再利用向量数量积求向量夹角,即得异面直线
,再利用向量数量积求向量夹角,即得异面直线![]() 与
与![]() 所成角,(2)先利用方程组解得平面
所成角,(2)先利用方程组解得平面![]() 的一个法向量,利用向量数量积得向量夹角余弦值,再根据线面角与向量夹角互余关系得结果,(3)先利用方程组解得平面
的一个法向量,利用向量数量积得向量夹角余弦值,再根据线面角与向量夹角互余关系得结果,(3)先利用方程组解得平面![]() 以及平面
以及平面![]() 的一个法向量,利用向量数量积得法向量夹角余弦值,再根据二面角与向量夹角相等或互补关系得结果.
的一个法向量,利用向量数量积得法向量夹角余弦值,再根据二面角与向量夹角相等或互补关系得结果.
详解:(1)当![]() 时,
时,![]() ,,
,,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
故 ,
,
所以异面直线![]() 与
与![]() 所成角为
所成角为![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,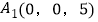 ,
,![]() ,
,
则![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则由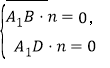 得,
得,![]()
不妨取![]() ,则
,则![]() , 此时
, 此时![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,因为
,因为![]() ,
,
则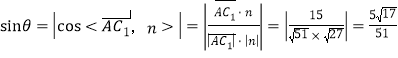 ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由![]() 得,
得,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则由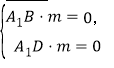 得,
得,![]()
不妨取![]() ,则
,则![]() , 此时
, 此时![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
故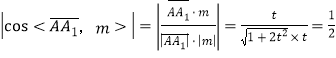 ,解得
,解得![]() ,
,
由图形得二面角![]() 大于
大于![]() ,所以符合题意.
,所以符合题意.
所以二面角![]() 的大小为
的大小为![]() ,
,![]() 的值为
的值为![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目


