题目内容
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
【答案】①③④
【解析】对于① 由向量![]() 满足
满足![]() ,由向量减法的三角形法则,知向量
,由向量减法的三角形法则,知向量![]() ,
, ![]() ,
, ![]() 组成一个等边三角形,向量
组成一个等边三角形,向量![]() ,
, ![]() 夹角为
夹角为![]() ,又由向量加法得平行四边形法则,以
,又由向量加法得平行四边形法则,以![]() ,
, ![]() 为邻边的平行四边形为菱形,所以
为邻边的平行四边形为菱形,所以![]() 的夹角为
的夹角为![]() ,故① 正 确;
,故① 正 确;
对于②,当![]() 时,不成立;
时,不成立;
对于③由![]()
则![]()
所以![]() ,即
,即![]() ,所以
,所以![]() 是直角三角形;
是直角三角形;
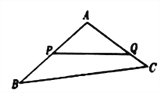
对于④由题目信息可作出如右图所示,三角形AOC为等边三角形,所以∠ACB=![]() ,且BC为直径,所以∠ABC=
,且BC为直径,所以∠ABC=![]()
在直角三角形ABC中BC=2,AC=1,所以AB=![]() ,
,
则向量![]() 在向量
在向量![]() 方向上的投影
方向上的投影![]() =
=![]() .
.
故④正确.

综上可知命题①③④正确.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |