题目内容
【题目】设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上，记 
．当∠APC为钝角时，则λ的取值范围是 ．
【答案】（ 
，1）
【解析】解：由题设，建立如图所示的空间直角坐标系D﹣xyz，则有A（1，0，0），B（1，1，0），C（0，1，0），D1（0，0，1）
∴ 
=（1，1，﹣1），∴ 
=（λ，λ，﹣λ），
∴ 
= 
+ 
=（﹣λ，﹣λ，λ）+（1，0，﹣1）=（1﹣λ，﹣λ，λ﹣1）
= + 
=（﹣λ，﹣λ，λ）+（0，1，﹣1）=（﹣λ，1﹣λ，λ﹣1）
显然∠APC不是平角，所以∠APC为钝角等价于cos∠APC＜0
∴ 
∴（1﹣λ）（﹣λ）+（﹣λ）（1﹣λ）+（λ﹣1）2=（λ﹣1）（3λ﹣1）＜0，得 ＜λ＜1
因此，λ的取值范围是（ ，1）
所以答案是：（ ，1）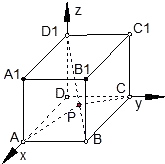
【考点精析】关于本题考查的用空间向量求直线间的夹角、距离，需要了解已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则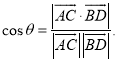
才能得出正确答案．
练习册系列答案
相关题目
