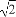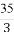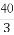题目内容
在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A,B,E,A1在一个平面内,AB=BC=CC1=2,AC=2 .
.

证明:(1)A1E∥AB.
(2)平面CC1FB⊥平面AA1EB.
见解析
【解析】【证明】(1)∵四边形ACC1A1是矩形,
∴A1C1∥AC.又AC?平面ABC,A1C1?平面ABC,
∴A1C1∥平面ABC.
∵FC1∥BC,BC?平面ABC,∴FC1∥平面ABC.
又∵A1C1,FC1?平面A1EFC1,
∴平面A1EFC1∥平面ABC.
又∵平面ABEA1与平面A1EFC1、平面ABC的交线分别是A1E,AB,∴A1E∥AB.
(2)∵四边形ACC1A1是矩形,∴AA1∥CC1.
∵∠BCC1=90°,即CC1⊥BC,∴AA1⊥BC.
又∵AB=BC=2,AC=2 ,∴AB2+BC2=AC2.
,∴AB2+BC2=AC2.
∴∠ABC=90°,即BC⊥AB.
∵AB,AA1?平面AA1EB,且AB∩AA1=A,
∴BC⊥平面AA1EB.
而BC?平面CC1FB,
∴平面CC1FB⊥平面AA1EB.

练习册系列答案
相关题目