若函数f(x)=a$\sqrt{x}$-x${\;}^{\frac{3}{2}}$+1不单调.则实数a的取值范围为a＞0．题目和参考答案——青夏教育精英家教网——

题目内容

9．若函数f（x）=a$\sqrt{x}$-x${\;}^{\frac{3}{2}}$+1不单调，则实数a的取值范围为a＞0．

分析换元，利用三次函数的单调性，可得结论．

解答解：令$\sqrt{x}$=t（t≥0），则y=-t³+at+1
∴y′=-3t²+a，
∵函数f（x）=a$\sqrt{x}$-x${\;}^{\frac{3}{2}}$+1不单调，
∴a＞0，
故答案为：a＞0．

点评本题考查了利用导数研究三次多项式函数的单调性，从而求参数a的取值范围，属于中档题，

练习册系列答案

优加学案口算题卡系列答案

全真模拟试卷精编系列答案

夺分A计划小学毕业升学总复习系列答案

小学毕业升学总复习金榜小状元系列答案

同步测评卷期末卷系列答案

小学生10分钟口算测试100分系列答案

小学6升7培优模拟试卷系列答案

名校秘题小学霸系列答案

孟建平小学毕业考试卷系列答案

层层递进系列答案

相关题目

19．已知数列{a_n}满足${S_n}=2{n^2}+n-1$，则通项a_n=$\left\{\begin{array}{l}2，n=1\\ 4n-1，n≥2\end{array}\right.$．

20．给定y与x的一组样本数据，求得相关系数r=-0.990，则（　　）

	A．	y与x负线性相关		B．	y与x正线性相关
	C．	y与x的线性相关性较强		D．	y与x的相关性很强

17．已知等式x²ⁿ=45^-3，则（　　）

x=45${\;}^{\frac{3}{2n}}$

x=45${\;}^{-\frac{2n}{3}}$

x=45${\;}^{-\frac{5}{n}}$

x²=45${\;}^{-\frac{3}{n}}$

4．关于x的方程2x²-3x-2k=0在（-1，1）内有一个实根，求实数k的取值范围．

14．已知关于x的方程2x²-（$\sqrt{3}+1$）x+m=0的两根sinθ和cosθ，θ∈（0，2π），求
（1）$\frac{si{n}^{2}θ}{sinθ-cosθ}$+$\frac{cosθ}{1-tanθ}$的值；
（2）实数m的值．
（3）方程的两根及此时θ的值．

1．已知一次函数f（x）=2x+b，幂函数g（x）=x^a，且知函数f（x）•g（x）的图象过（1，2），函数$\frac{f（x）}{g（x）}$的图象过（$\sqrt{2}$，1），若函数h（x）=（（g（x））${\;}^{\frac{1}{3}}$•（$\frac{1}{2}$f（x））${\;}^{-\frac{1}{3}}$．
（1）证明函数h（x）为幂函数．
（2）判断函数h（x）的奇偶性．

18．计算：（1）log₉3+log₉27=2；
（2）log₂$\frac{1}{2}$+$lo{g}_{\frac{1}{2}}2$=-2．

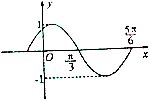如图函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}$）图象的一部分，则f（$\frac{π}{4}$）的值为$\frac{1}{2}$．