Question

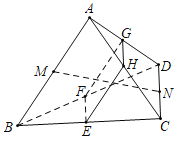
【题目】如图，在棱长为1的正四面体ABCD中，M，N分别为棱AB和CD的中点，一个平面分别与棱BC，BD，AD，AC交于E，F，G，H，且MN⊥平面EFGH.给出下列六个结论：①AC⊥BD，②AB//平面EFGH，③平面ABC⊥平面EFGH，④四边形EFGH的周长为定值；⑤四边形EFGH的面积有最大值；⑥四边形EFGH一定是矩形，其中，所有正确结论的序号是_____.

Answer 1

【答案】①②④⑤⑥

【解析】

利用正四面体的性质判断①；利用直线与平面垂直的性质判断②；平面是否垂直判断③；通过折叠与展开判断④；求出四边形的面积判断⑤；判断四边形的形状判断⑥；

在棱长为1的正四面体中，对棱垂直，所以①，正确；

，分别为棱和的中点，可知，，

一个平面分别与棱，，，交于，，，，且平面．

所以，平面，所以②正确；

同时，所以四边形一定是矩形，所以⑥正确；

平面平面，所以平面平面不正确，即③不正确；

由比例关系可知：是定值，四边形的周长为定值2，④正确；

由基本不等式的形状，可知四边形的面积有最大值1；所以⑤正确；

故答案为：①②④⑤⑥．