题目内容
【题目】设函数 若
若![]() ,则
,则![]() 的最小值为__________; 若
的最小值为__________; 若![]() 有最小值,则实数
有最小值,则实数![]() 的取值范围是_______.
的取值范围是_______.
【答案】![]()
![]()
【解析】
(1)将a=1代入函数,分析每段函数的最小值,则![]() 的最小值可求;(2)讨论a<0,a=0和a>0时函数的单调性和最小值即可求解
的最小值可求;(2)讨论a<0,a=0和a>0时函数的单调性和最小值即可求解
(1)当a=1,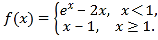 ,
,![]() =
=![]() (
(![]() )=
)=![]() (
(![]() )>0,1>x>ln2;
)>0,1>x>ln2;![]() (
(![]() )<0,x<ln2;故
)<0,x<ln2;故![]() 当
当![]() =
=![]() ,
,![]() 单调递增,故
单调递增,故![]() ,又
,又![]() 所以
所以![]() 的最小值为0
的最小值为0
(2) ①当a<0时,由(1)知![]() =
=![]() 单调递减,故
单调递减,故![]() (
(![]() )单调递减,故
)单调递减,故![]() 故
故![]() 无最小值,舍去;
无最小值,舍去;
②当a=0时,f(x)最小值为-1,成立
③当a>0时,![]() (
(![]() )单调递增,故
)单调递增,故![]()
对![]() =
=![]() ,
,
当0<a![]() ln2,由(1)知
ln2,由(1)知![]() ,此时
,此时 最小值在x=a处取得,成立
最小值在x=a处取得,成立
当a>ln2, 由(1)知![]() ,此时
,此时 最小值为
最小值为![]() ,即
,即![]() 有最小值,综上a
有最小值,综上a![]()
故答案为![]() ;
; ![]()

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目


