Question

2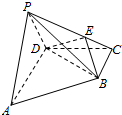．如图，四棱锥P-ABCD中，AD∥BC，AD⊥DC，AD=2BC=2CD=2，侧面APD为等腰直角
三角形，PA⊥PD，平面PAD⊥底面ABCD，E为侧棱PC上不同于端点的一点．
（1）证明：PA⊥DE；
（2）试确定点E的位置，使二面角E-BD-C的余弦值为$\frac{{\sqrt{3}}}{3}$．

Answer 1

分析 （1）通过AD⊥DC，平面PAD⊥底面ABCD，及面面垂直的性质定理可得DC⊥PA，利用PA⊥PD及线面垂直的判定定理、性质定理即得结论；
（2）以P为坐标原点，分别以PA、PD所在直线为x、y轴建系P-xyz．利用$\overrightarrow{PE}$与$\overrightarrow{PC}$共线，可设E（0，$\sqrt{2}$q，q），利用平面BCD的法向量与平面BDE的法向量的夹角的余弦值为$\frac{\sqrt{3}}{3}$，计算可得q=$\frac{2}{3}$，进而可得结论．

解答 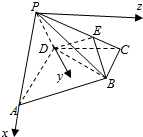（1）证明：∵AD⊥DC，平面PAD⊥底面ABCD，
∴DC⊥平面PAD，∴DC⊥PA，
又∵PA⊥PD，∴PA⊥平面PCD，
∴PA⊥DE；
（2）解：以P为坐标原点，分别以PA、PD所在直线为x、y轴建系P-xyz如图．
∵AD=2BC=2CD=2，侧面APD为等腰直角，∴PD=PA=$\sqrt{2}$，
∴P（0，0，0），B（$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$，1），C（0，$\sqrt{2}$，1），D（0，$\sqrt{2}$，0），
设E（0，p，q），显然$\overrightarrow{PE}$与$\overrightarrow{PC}$共线，∴（0，p，q）=λ（0，$\sqrt{2}$，1），
即p=$\sqrt{2}$q，则E（0，$\sqrt{2}$q，q），
则$\overrightarrow{DB}$=（$\frac{\sqrt{2}}{2}$，-$\frac{\sqrt{2}}{2}$，1），$\overrightarrow{DE}$=（0，$\sqrt{2}$q-$\sqrt{2}$，q），$\overrightarrow{DC}$=（0，0，1），
设平面BCD的法向量为$\overrightarrow{m}$=（x，y，z），
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DB}=0}\\{\overrightarrow{m}•\overrightarrow{DC}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}y+z=0}\\{z=0}\end{array}\right.$，
取x=1，得$\overrightarrow{m}$=（1，1，0），
设平面BDE的法向量为$\overrightarrow{n}$=（x，y，z），
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=0}\\{\overrightarrow{n}•\overrightarrow{DE}=0}\end{array}\right.$，得$\left\{\begin{array}{l}{\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}y+z=0}\\{\sqrt{2}（q-1）y+qz=0}\end{array}\right.$，
取x=2，得$\overrightarrow{n}$=（2，$\frac{2q}{3q-2}$，$\frac{2\sqrt{2}（1-q）}{3q-2}$），
∵cos＜$\overrightarrow{m}$，$\overrightarrow{n}$＞=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2+\frac{2q}{3q-2}}{\sqrt{2}•2\sqrt{2}•\frac{\sqrt{6{q}^{2}-8q+3}}{3q-2}}$=$\frac{\sqrt{3}}{3}$，
化简得：$\frac{2q-1}{\sqrt{6{q}^{2}-8q+3}}$=$\frac{\sqrt{3}}{3}$，解得q=$\frac{2}{3}$或q=0（舍去），
∴E（0，$\frac{2}{3}$$\sqrt{2}$，$\frac{2}{3}$），即点E位于靠近C点的三等分点处．

点评 本题考查线线垂直的判定，考查二面角的三角函数值，注意解题方法的积累，属于中档题．