题目内容
【题目】在三棱锥DABC中,ADDC,ACCB,AB=2AD=2DC=2,且平面ABD平面BCD,E为AC的中点.
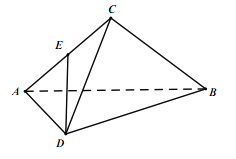
(I)证明:ADBC;
(II)求直线 DE 与平面ABD所成的角的正弦值.
【答案】(I)见证明;(II)![]()
【解析】
(I)先作![]() ,由面面垂直的性质定理可证线面垂直,再结合条件证得
,由面面垂直的性质定理可证线面垂直,再结合条件证得![]() 面
面![]() ,得到结论.
,得到结论.
(II)法一:根据(1)作出过E且与CH平行的线段,可得到线面角,再在直角三角形中求解即可. 法二:以D为坐标原点建立空间直角坐标系,求出![]() 和平面ABD的法向量
和平面ABD的法向量![]() ,则|cos
,则|cos![]() |即为所求.
|即为所求.
(I)过![]() 作
作![]() ,(其中
,(其中![]() 与
与![]() 都不重合,否则,若
都不重合,否则,若![]() 与
与![]() 重合,则
重合,则![]() 与
与![]() 矛盾,
矛盾,
若![]() 与
与![]() 重合,则
重合,则![]() ,与
,与![]() 矛盾)
矛盾)
![]() 面
面![]() 面
面![]()
![]()
![]() 面
面![]()
![]()
![]()
![]() ,又
,又![]()
![]()
![]()
![]()
![]() 面
面![]()
![]()
![]()
![]()
(II)法一:作![]() ,则
,则![]() ,
,
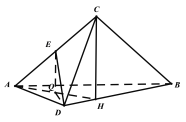
由(1)知:![]() 面
面![]()
![]()
![]() 即
即![]() 与面
与面![]() 所成角,且
所成角,且![]()
![]()
![]()
法二:由(I)知![]() 平面
平面![]() ,
,![]() ,以
,以![]() 为原点,分别以射线
为原点,分别以射线![]() 为
为![]() 轴,
轴,![]() 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系![]()
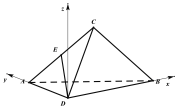
由题意知:![]()
∴![]() ,
,![]()
∵平面![]() 的法向量为
的法向量为![]() ,
,
设![]() 与面
与面![]() 所成角为
所成角为![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目