题目内容
掷甲、乙两颗骰子,甲出现的点数为 ,乙出现的点数为
,乙出现的点数为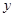 ,若令
,若令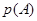 为
为 的概率,
的概率,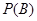 为
为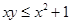 的概率,试求
的概率,试求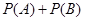 的值.
的值.
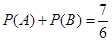 .
.
解析试题分析:由题意可知事件 为
为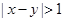 ,因此考虑通过求其对立事件
,因此考虑通过求其对立事件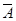
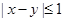 发生的概率
发生的概率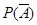 来求
来求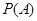 ,穷举易得事件
,穷举易得事件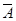 包含了
包含了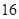 个基本事件,因此
个基本事件,因此 ,而事件
,而事件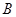 为
为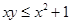 ,变形即
,变形即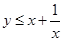 ,同样通过穷举可知事件
,同样通过穷举可知事件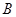 包含了
包含了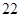 个基本事件,因此
个基本事件,因此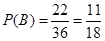 ,
,
从而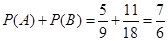 .
.
试题解析:以有序实数对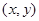 来表示两次抛掷骰子的结果,则总共有
来表示两次抛掷骰子的结果,则总共有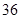 个基本事件,根据题意,事件
个基本事件,根据题意,事件 为
为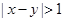 ,则事件
,则事件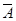 为
为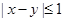 ,总共有
,总共有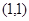 ,
,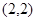 ,……
,……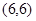 ,
,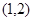 ,
,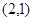 ,
, ,
,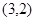 ,……
,……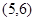 ,
,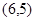
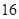 个基本事件,根据古典概型可知
个基本事件,根据古典概型可知 ,同理事件
,同理事件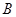 为
为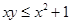 ,即
,即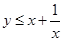 ,若
,若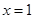 ,
,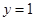 ,
,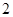 ;若
;若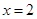 ,
,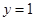 ,
,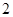 ;若
;若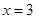 ,
,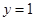 ,
,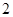 ,
,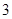 ;若
;若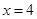 ,
,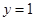 ,
,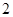 ,
,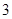 ,
,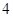 ;若
;若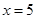 ,
,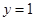 ,
,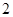 ,
,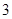 ,
,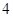 ,
,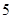 ;若
;若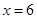 ,
,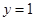 ,
,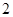 ,
,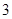 ,
,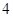 ,
,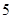 ,
,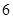 ,
,
∴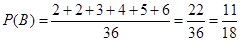 ,∴
,∴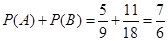 .
.
考点:古典概型求概率.

练习册系列答案
相关题目
某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差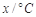 | 10 | 11 | 13 | 12 | 8 |
发芽数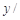 颗 颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为
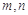 ,求事件“
,求事件“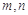 均不小于25的概率。
均不小于25的概率。(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出
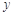 关于
关于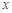 的线性回归方程
的线性回归方程 ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:
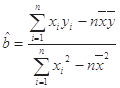 ,
,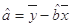 )
) 
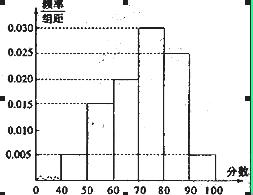
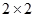 列联表:
列联表: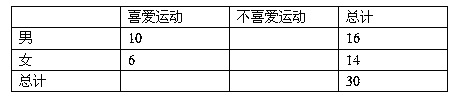
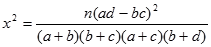 (其中
(其中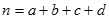 )
)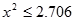
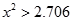

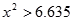
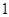 的球
的球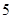 个,编号为
个,编号为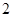 的球
的球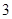 个,这些球的大小完全一样。
个,这些球的大小完全一样。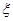 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量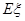 .
. .
.
