题目内容
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:(Ⅰ)连续取两次都是白球的概率;(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.
(1) ;(2)
;(2)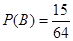
解析试题分析:(1)从4个球中有放回地连续抽取2个,共有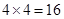 ,而两次都是白球的种数有:
,而两次都是白球的种数有: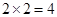 ,然后由古典概型计算可得结果
,然后由古典概型计算可得结果 ;(2)连续三次共有
;(2)连续三次共有 ,其中出现4分,则含有的类型有:1红2白,共有
,其中出现4分,则含有的类型有:1红2白,共有 ;2红1黑,共有
;2红1黑,共有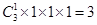 ,故共有
,故共有 ,由古典概型计算可得结果
,由古典概型计算可得结果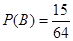 .本题(1)(2)小问也可以采用列举法(列举出所有结果)得到,见下列解析.
.本题(1)(2)小问也可以采用列举法(列举出所有结果)得到,见下列解析.
试题解析:(1)设连续取两次的事件总数为 :(红,红),(红,白1),(红,白2),(红,黑);(白1,红)(白1,白1)(白1,白2),(白1,黑);(白2,红),(白2,白1),(白2,白2),(白2,黑);(黑,红),(黑,白1),(黑,白2),(黑,黑),所以
:(红,红),(红,白1),(红,白2),(红,黑);(白1,红)(白1,白1)(白1,白2),(白1,黑);(白2,红),(白2,白1),(白2,白2),(白2,黑);(黑,红),(黑,白1),(黑,白2),(黑,黑),所以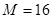 .
.
设事件A:连续取两次都是白球,(白1,白1)(白1,白2),(白2,白1),(白2,白2)共4个,
所以, .
.
(2)连续取三次的基本事件总数为N:(红,红,红),(红,红,白1),(红,红,白2),(红,红,黑),有4个;(红,白1,红),(红,白1,白1),等等也是4个,如此,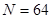 个;
个;
设事件B:连续取三次分数之和为4分;因为取一个红球记2分,取一个白球记1分,取一个黑球记0 分,则连续取三次分数之和为4分的有如下基本事件:
(红,白1,白1),(红,白1,白2),(红,白2,白1),(红,白2,白2),
(白1,红,白1),(白1,红,白2),(白2,红,白1),(白2,红,白2),
(白1,白1,红),(白1,白2,红),(白2,白1,红),(白2,白2,红),
(红,红,黑),(红,黑,红),(黑,红,红),共15个基本事件,
所以,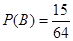 .
.
考点:(1)古典概型;(2)分步计数原理.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案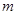 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为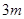 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为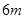 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是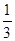 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?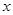 的一元二次方程
的一元二次方程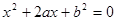
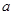 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,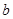 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;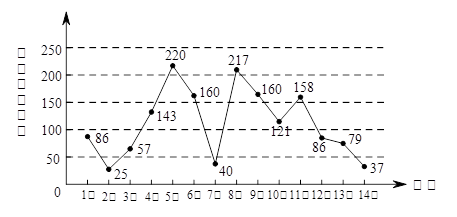
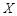 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。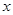 ,乙出现的点数为
,乙出现的点数为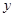 ,若令
,若令 为
为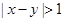 的概率,
的概率,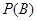 为
为 的概率,试求
的概率,试求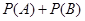 的值.
的值.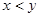 ”
”