题目内容
某校从高一年级周末考试的学生中抽出6O名学生,其成绩(均为整数)的频率分布直方图如图所示:(1)依据频率分布直方图,估计这次考试的及格率(60分及以上为及格)和平均分;(2)已知在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,96,97,98,99,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.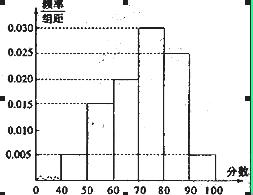
(1)80%,72分;(2)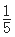
解析试题分析:(1)本小题要求的及格率只需找到60分及以上的各组频率和(或60分及以上的各组对应的长方形总面积)即可,也就是从图中可看出的每组长方形的高(其值为 )与各组的组距相乘之和;平均分即为这组数据的平均数,只要把每组的组中值乘以每组的频率再相加即可;(2)本小题中从95,96,97,98,99,100中抽取2个数,总的基本事件的数目为15个,而[90,100]分数段内学生数为0.005×10×60=3人,这3人成绩都不相同且都在94分以上,则可设他们的成绩是95,96,97,又“2个数恰好是两个学生的成绩”含的基本事件的数目为3,故所求概率为
)与各组的组距相乘之和;平均分即为这组数据的平均数,只要把每组的组中值乘以每组的频率再相加即可;(2)本小题中从95,96,97,98,99,100中抽取2个数,总的基本事件的数目为15个,而[90,100]分数段内学生数为0.005×10×60=3人,这3人成绩都不相同且都在94分以上,则可设他们的成绩是95,96,97,又“2个数恰好是两个学生的成绩”含的基本事件的数目为3,故所求概率为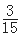 即为
即为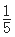 .
.
试题解析:(1)由图知,60及以上的分数所在的第三、四、五、六组的频率和为(0.020+0.030+0.025+0.005)×10=0.80所以,抽样学生成绩的合格率是80%.利用组中值估算抽样学生的平均分: =45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05=72,所以,估计这次考试的平均分是72分.
=45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05=72,所以,估计这次考试的平均分是72分.
(2)从95,96,97,98,99,100中抽取2个数,全部可能的基本事件有:(95,96),(95,97),(95,98),(95,99),(95,100),(96,98),(96,99),(96,100),(97,98),(97,99),(97,100),(98,99),(98,100),(99,100),共15个基本事件. 如果这2个数恰好是两个学生的成绩,则这2个学生在[90,100]段,而[90,100]的人数是3人,不妨设这3人的成绩是95,96,97. 则事件A:“2个数恰好是两个学生的成绩”包括的基本事件:(95,96),(95,97),(96,97).共有3个基本事件.所以所求的概率为P(A)=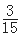 =
=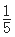 .
.
考点:频率分布直方图中每组的频率(即每个长方形的面积)为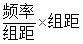 ,数据的平均数=每组的组中值乘以每组的频率再相加;基本事件的概念,古典概型的概率计算公式.
,数据的平均数=每组的组中值乘以每组的频率再相加;基本事件的概念,古典概型的概率计算公式.

我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
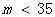 | 一级 |
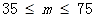 | 二级 |
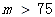 | 超标 |
某市环保局从180天的市区PM2.5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).

(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记
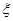 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求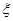 的分布列;
的分布列;(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级.
 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为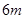 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?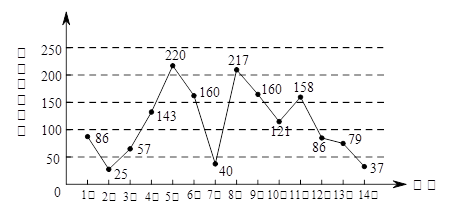
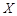 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。 ,乙出现的点数为
,乙出现的点数为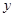 ,若令
,若令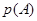 为
为 的概率,
的概率,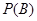 为
为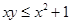 的概率,试求
的概率,试求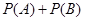 的值.
的值. 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为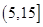 ,
,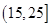 ,
,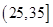 ,
,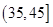 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.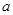 的值;
的值; 组的频率为
组的频率为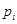 ,第
,第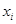
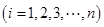 ,则样本数据的平均值为
,则样本数据的平均值为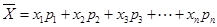 .)
.) ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取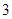 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为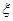 ,求
,求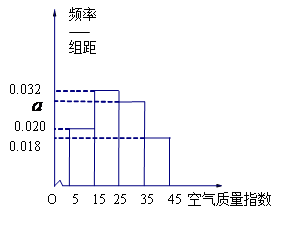
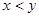 ”
”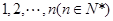 从小到大排列构成一个数
从小到大排列构成一个数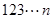 ,
,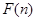 为这个数的位数(如
为这个数的位数(如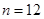 时,此数为
时,此数为 ,共有15个数字,
,共有15个数字, ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,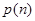 为恰好取到0的概率.
为恰好取到0的概率.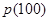 ;
;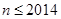 时,求
时,求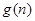 为这个数中数字0的个数,
为这个数中数字0的个数,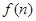 为这个数中数字9的个数,
为这个数中数字9的个数,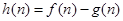 ,
, ,求当
,求当 时
时