题目内容
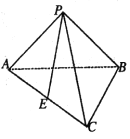
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() ,
, ![]() ,知
,知![]() .由
.由![]() ,
, ![]() 是
是![]() 的中点,知四边形
的中点,知四边形![]() 是平行四边形,由此能证明线面平行;(2)先证知
是平行四边形,由此能证明线面平行;(2)先证知![]() 两两垂直.以点
两两垂直.以点![]() 为坐标原点,
为坐标原点, ![]() 分别为
分别为![]() 轴建立空间直角坐标系,利用向量法能够求出二面角
轴建立空间直角坐标系,利用向量法能够求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:∵![]() ,
, ![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
, ![]() 是
是![]() 的中点,∴
的中点,∴![]() ,且
,且![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() .∵
.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
, ![]() ,又
,又![]() ,∴
,∴![]() 两两垂直,以点
两两垂直,以点![]() 为坐标原点,
为坐标原点, ![]() 分别为
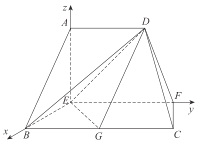
分别为![]() 轴,建立如图的空间直角坐标系,由已知得
轴,建立如图的空间直角坐标系,由已知得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由已知得
,由已知得![]() 是平面
是平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,∵
,∵![]() ,
, ![]() ,∴
,∴![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() .设二面角
.设二面角![]() 的大小为
的大小为![]() .
. ![]() ,∴二面角
,∴二面角![]() 的余弦值为
的余弦值为![]() .
.

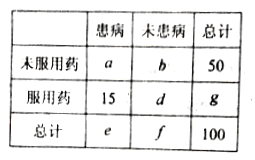
【题目】某养鸡场为检验某种药物预防某种疾病的效果,取100只鸡进行对比试验,得到如下列联表(表中部分数据丢失, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 表示丢失的数据):
表示丢失的数据):
工作人员记得![]() .
.
(1)求出列联表中数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)能否在犯错误的概率不超过0.005的前提下认为药物有效?
参考公式: 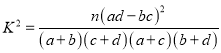 ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |