题目内容
已知函数 .
.
(Ⅰ)当 ,函数
,函数 有且仅有一个零点
有且仅有一个零点 ,且
,且 时,求
时,求 的值;
的值;
(Ⅱ)若函数 在区间
在区间 上为单调函数,求
上为单调函数,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) 或
或 .
.
解析试题分析:(1)由 可求出
可求出 的值,然后将
的值,然后将 有且仅有一个零点
有且仅有一个零点 ,且
,且 ,转化函数
,转化函数 的图像与直线
的图像与直线 有且只有一个交点,最后根据图像可得出
有且只有一个交点,最后根据图像可得出 的值;(2)针对
的值;(2)针对 进行分类:
进行分类: 、
、 、
、 并结合双勾函数的单调性可求得
并结合双勾函数的单调性可求得 的取值范围.
的取值范围.
试题解析:(Ⅰ)
 ,得
,得 , 3分
, 3分 ,作出该函数的图像
,作出该函数的图像
 函数
函数 有且仅有一个零点
有且仅有一个零点 ,且
,且
 由图像可知,函数
由图像可知,函数 的图像与直线
的图像与直线 有且只有一个交点,且交点的横坐标为
有且只有一个交点,且交点的横坐标为 6分
6分 8分
8分
(Ⅱ)若 ,则函数
,则函数 在区间
在区间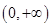 上单调递增,满足题意;
上单调递增,满足题意;
若 ,则
,则 ,也满足题意; 10分
,也满足题意; 10分
若 ,则函数
,则函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,则要满足函数
上单调递增,则要满足函数 在区间
在区间 上为单调函数,则
上为单调函数,则 或
或 ,
,
得 或
或 14分
14分
所以,综上所述,得, 的取值范围是
的取值范围是 或
或 16分.
16分.
考点:1.函数的零点;2.函数的单调性;3.分类讨论的思想.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
 的定义域;
的定义域; 的定义域为
的定义域为 .设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
.设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N. 是定值;
是定值; 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值. 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 ,
, .
.  为奇函数,求实数
为奇函数,求实数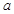 的值;
的值; 上的所有上界构成的集合;
上的所有上界构成的集合; 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时有
时有 .
.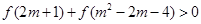 ,求
,求 的取值范围.
的取值范围.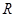 的函数
的函数
 的图象,并指出
的图象,并指出 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明). 为奇函数,且当
为奇函数,且当 时,
时, 求
求
 ,
, ,求方程
,求方程 的根;
的根; 满足
满足 ,求函数在
,求函数在 的值域.
的值域. (
( 为实常数).
为实常数). 图像上动点
图像上动点 到定点
到定点 的距离的最小值为
的距离的最小值为 ,求实数
,求实数 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数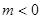 ,若不等式
,若不等式 在
在 有解,求
有解,求 的取值范围.
的取值范围. 同时满足以下三个条件时称
同时满足以下三个条件时称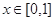 ,总有
,总有 ;
; 成立,则下列判断正确的有 .
成立,则下列判断正确的有 . ;
; 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”; <
< ≤1,则
≤1,则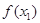 ≤
≤ .
.