题目内容
【题目】已知两点M和N分别在直线y=mx和y=﹣mx（m＞0）上运动，且|MN|=2，动点p满足： 
（O为坐标原点），点P的轨迹记为曲线C． （I）求曲线C的方程，并讨论曲线C的类型；
（Ⅱ）过点（0，1）作直线l与曲线C交于不同的两点A、B，若对于任意m＞1，都有∠AOB为锐角，求直线l的斜率k的取值范围．
【答案】解：（I）由 
，得P是MN的中点． 设P（x，y），M（x1 ， mx1），N（x2 ， ﹣mx2）依题意得：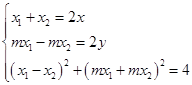
消去x1 ， x2 ， 整理得 
．
当m＞1时，方程表示焦点在y轴上的椭圆；
当o＜m＜1时，方程表示焦点在x轴上的椭圆；
当m=1时，方程表示圆．
（II）由m＞1，焦点在y轴上的椭圆，直线l与曲线c恒有两交点，
因为直线斜率不存在时不符合题意，
可设直线l的方程为y=kx+1，直线与椭圆的交点为A（x1 ， y1），B（x2 ， y2）．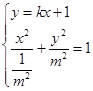
（m4+k2）x2+2kx+1﹣m2=0
， 
要使∠AOB为锐角，则有 
∴x1x2+y1y2= 
即m4﹣（k2+1）m2+1＞0，
可得 
，对于任意m＞1恒成立．
而 
，∴K2+1≤2，﹣1≤k≤1
所以满足条件的k的取值范围是[﹣1.1]
【解析】（I）根据题意可判断出P是MN的中点．设出P，M，N的坐标，根据题意联立方程求得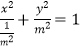 
，然后对m＞1，o＜m＜1和m=1对方程表示出曲线进行分类讨论．（II）设出直线l的方程，与椭圆的方程联立消去y，利用韦达定理表示出x1+x2和x1x2 ， 利用直线方程表示出y1y2 ， 要使∠AOB为锐角，需 
，利用向量的基本运算整理得 
，利用基本不等式求得 
进而求得k的范围．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
