题目内容

1．求函数f（x）=|sinx|+|cosx|的最小正周期．

分析 首先把三角函数变形成f（x）=$\sqrt{1+|sin2x|}$的形式，进一步求出函数的最小正周期，

解答 解：∵函数f（x）=|sinx|+|cosx|=$\sqrt{1+|sin2x|}$，
∴最小正周期T=$\frac{π}{2}$．

点评 本题主要考查了三角函数恒等变换的应用，考查了三角函数的周期性及其求法，求得|sinx|+|cosx|=$\sqrt{1+|sin2x|}$是解题的关键，属于基本知识的考查．

练习册系列答案
相关题目
6．已知向量$\overrightarrow{a}$=（$\sqrt{3}$sinx，cosx），$\overrightarrow{b}$=（cosx，cosx），函数f（x）=2$\overrightarrow{a}$•$\overrightarrow{b}$-1
（1）求f（x）的单调递增区间；
（2）当x∈[$\frac{π}{6}$，$\frac{π}{2}$]时，若f（x）=1，求x的值．
12．已知函数f（x）=cos（ωx+θ）为奇函数（0＜θ＜π），其图象与直线y=1的某两个交点的横坐标分别为x1、x2，且|x2-x1|的最小值为π，则（　　）
A．$ω=2，θ=\frac{π}{2}$B．$ω=\frac{1}{2}，θ=\frac{π}{2}$C．$ω=\frac{1}{2}，θ=\frac{π}{4}$D．$ω=2，θ=\frac{π}{4}$
9．设定义在R上的奇函数f（x）在区间（0，+∞）上单调递增，则不等式f（x-1）＜0的解集是（　　）
A．（-∞，1）B．（1，+∞）C．（0，+∞）D．（-∞，0）
16．已知函数f（x）=cos（2x-$\frac{π}{3}$）-2sin2x+1．
（1）求函数f（x）的最小正周期；
（2）求函数f（x）在[0，π]上的单调增区间．
6．如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（　　）
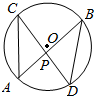
A．38°B．42°C．80°D．118°
13．已知f（x）=$\left\{\begin{array}{l}x+2\;\;\;\;\;x＜2\\ \frac{x^2}{2}\;\;\;\;\;\;\;x≥2\end{array}$
（1）求f[f（0）]；
（2）若f（a）=3，求a．
10．204与85的最大公约数是17．
11．已知cosα=$\frac{\sqrt{5}}{5}$，sin（α-β）=$\frac{\sqrt{10}}{10}$，且α、β∈（0，$\frac{π}{2}$）．求：
（Ⅰ）cos（2α-β）的值；  
（Ⅱ）β的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网