题目内容
【题目】已知数列{an}的前n项和Sn=10n﹣n2(n∈N*),又bn=|an|(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn .
【答案】
(1)解:∵数列{an}的前n项和Sn=10n﹣n2(n∈N*),
∴当n=1时,a1=S1=9,当n≥2时,an=Sn﹣Sn﹣1=10n﹣n2﹣[10(n﹣1)﹣(n﹣1)2]=11﹣2n.
当n=1时上式也成立,
∴an=11﹣2n.
(2)解:由an=11﹣2n≥0,解得n≤5.
∴bn=|an|= ![]() .
.
∴当n≤5时,Tn=Sn=10n﹣n2.
当n≥6时,Tn=2S5﹣Sn
=2×(10×5﹣52)﹣(10n﹣n2)
=n2﹣10n+50.
∴Tn= ![]()
【解析】(1)数列{an}的前n项和Sn=10n﹣n2(n∈N*),当n=1时,a1=S1=9,当n≥2时,an=Sn﹣Sn﹣1 , 即可得出.(2)由an=11﹣2n≥0,解得n≤5.可得bn=|an|= ![]() .当n≤5时,Tn=Sn . 当n≥6时,Tn=2S5﹣Sn , 即可得出.
.当n≤5时,Tn=Sn . 当n≥6时,Tn=2S5﹣Sn , 即可得出.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系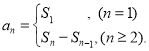 .
.

【题目】某小型工厂安排甲、乙两种产品的生产,已知工厂生产甲、乙两种产品每吨所需要的原材料A,B,C的数量和一周内可用资源数量如下表所示:
原材料 | 甲(吨) | 乙(吨) | 资源数量(吨) |
A | 1 | 1 | 50 |
B | 4 | 0 | 160 |
C | 2 | 5 | 200 |
如果甲产品每吨的利润为300元,乙产品每吨的利润为200元,那么适当安排生产后,工厂每周可获得的最大利润为______元.
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.

