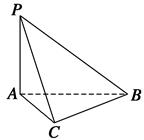
题目内容
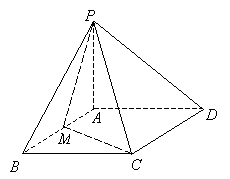
(本题满分10分)如图,在四棱锥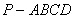 中,底面
中,底面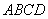 是边长为2的正方形,且
是边长为2的正方形,且 ,
,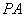 =
=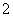 ,
,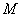 为
为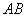 的中点. 求:
的中点. 求:
(Ⅰ) 异面直线CM与PD所成的角的余弦值;
(Ⅱ)直线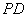 与平面
与平面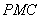 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面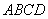 是边长为2的正方形,且
是边长为2的正方形,且 ,
,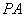 =
=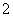 ,
,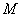 为
为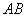 的中点. 求:
的中点. 求:(Ⅰ) 异面直线CM与PD所成的角的余弦值;
(Ⅱ)直线
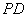 与平面
与平面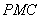 所成角的正弦值.
所成角的正弦值.
20. 解:如图,以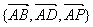 为一组基底建立空间直角坐标系,
为一组基底建立空间直角坐标系,
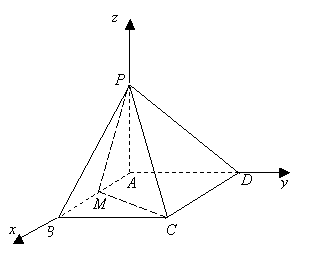
由题可知,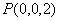 ,
,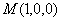 ,
,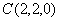 ,
,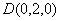
( I )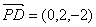 ,
,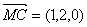
设直线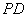 与直线
与直线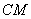 所成角为
所成角为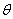 ,则
,则
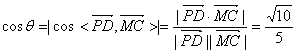
( II )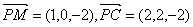
设平面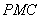 的法向量为
的法向量为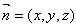
因为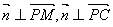 ,则
,则
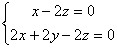 ,所以
,所以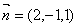
设直线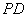 与平面
与平面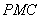 所成的角为
所成的角为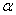 ,
,
所以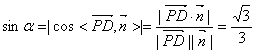
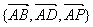 为一组基底建立空间直角坐标系,
为一组基底建立空间直角坐标系,
由题可知,
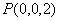 ,
,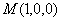 ,
,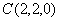 ,
,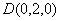
( I )
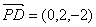 ,
,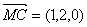
设直线
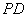 与直线
与直线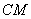 所成角为
所成角为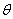 ,则
,则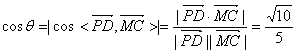
( II )
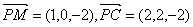
设平面
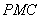 的法向量为
的法向量为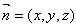
因为
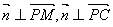 ,则
,则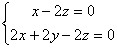 ,所以
,所以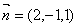
设直线
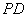 与平面
与平面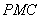 所成的角为
所成的角为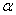 ,
,所以
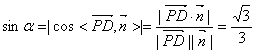
略

练习册系列答案
相关题目
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,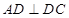 ,
,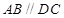 ,
,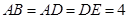 ,
,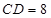 .
. 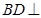 平面
平面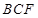 ;
;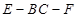 的平面角为
的平面角为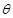 ,求
,求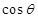 的值;
的值;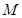 为
为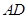 的中点,在
的中点,在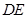 上是否存在一点
上是否存在一点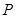 ,使得
,使得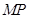 ∥平面
∥平面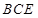 ?若存在,求出
?若存在,求出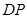 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.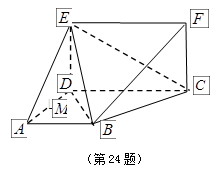
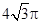 的球的内接正方体的棱长为_____________。
的球的内接正方体的棱长为_____________。 中,
中,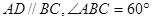 ,
,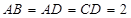 ,
,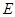 为
为 中点.将
中点.将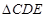 沿
沿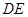 折起至
折起至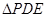 ,使得平面
,使得平面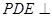 平面
平面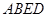 ,
,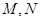 分别为
分别为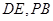 的中点.
的中点.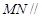 面
面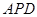 ;
;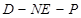 的余弦值.
的余弦值.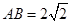 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.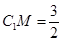 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.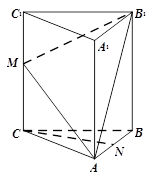
 为矩形,
为矩形, 平面
平面 ,
,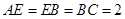 ,
,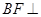 平面
平面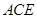 于点
于点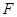 ,且点
,且点 上.
上.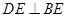 ;
;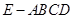 的体积;
的体积;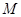 在线段
在线段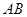 上,且
上,且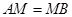 ,
,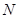 ,使得
,使得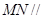 平面
平面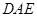 .
.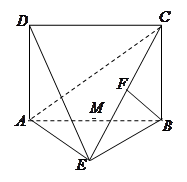
 B
B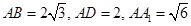 ,则点
,则点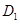 到直线AC的距离是
到直线AC的距离是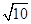
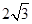
 ,G、H分别是BE、ED的中点,则GH到平面ABD的距离是______
,G、H分别是BE、ED的中点,则GH到平面ABD的距离是______ 平面PAC;
平面PAC;