题目内容
3.任意确定四个日期,其中至少有两个是星期天的概率为( )| A. | $\frac{241}{2401}$ | B. | $\frac{1105}{2401}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{7}$ |
分析 记“取到的日期为星期天”为事件A,则P(A)=$\frac{1}{7}$,利用n次独立重复试验中事件A恰好发生k次的概率计算公式求出任意确定四个日期中星期天的个数为0个和1个的概率,由此利用对立事件概率计算公式能求出任意确定四个日期,其中至少有两个是星期天的概率.
解答 解:记“取到的日期为星期天”为事件A,则P(A)=$\frac{1}{7}$,
设Ai表示取到的四个日期中有i个星期天(i=0,1,2,3,4),
则P(A0)=${C}_{4}^{0}(\frac{1}{7})^{0}×(1-\frac{1}{7})^{4}$,
$P({A}_{1})={C}_{4}^{1}(\frac{1}{7})(1-\frac{1}{7})^{3}$=$\frac{864}{2401}$,
∴任意确定四个日期,其中至少有两个是星期天的概率为:
p=1-[P(A0)+p(A1)]
=1-($\frac{1296}{2401}+\frac{864}{2401}$)
=$\frac{241}{2401}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式和对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
11.有一几何体的三视图如图,则该几何体体积为( )
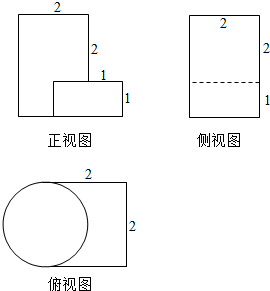

| A. | 4+$\frac{5π}{2}$ | B. | 4+$\frac{3π}{2}$ | C. | 4+$\frac{π}{2}$ | D. | 4+π |
12.已知随机变量ξ的分布列如下:
则P(2≤ξ<4)=0.6.
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.2 | 0.4 | 0.2 | 0.1 |