题目内容
6.已知圆M:x2+y2-2mx-2my+m2=0与圆N:x2+y2+2x+2y=0交于A,B两点,且这两点平分圆N的周长,求圆M的方程.分析 由题意在Rt△AMN中,|AM|2=|AN|2+|MN|2,求圆M的圆心坐标,即可求圆M的方程.
解答 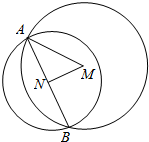 解:由题意,圆M的圆心坐标为M(m,m),半径为|m|
解:由题意,圆M的圆心坐标为M(m,m),半径为|m|
圆N的圆心N(-1,-1),半径为$\sqrt{2}$,N为弦AB的中点,
在Rt△AMN中,|AM|2=|AN|2+|MN|2,
∴m2=2+(m+1)2+(m+1)2,
∴m=-2,
∴圆M的圆心坐标为(-2,-2).圆M的方程为(x+2)2+(y+2)2=4.
点评 本小题主要考查圆与圆的位置关系,考查运用数学知识解决问题的能力,比较基础.

练习册系列答案
相关题目
18.线段P1P2长为5cm,点P在P1P2的延长线上,且|P2P|=5cm,则点P分$\overrightarrow{{P}_{2}{P}_{1}}$所成的比是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
 在空间直角坐标系中有单位正方体ABCD-A′B′C′D′,E,F分别是棱C′D′和B′C′的中点,试求:
在空间直角坐标系中有单位正方体ABCD-A′B′C′D′,E,F分别是棱C′D′和B′C′的中点,试求: