题目内容
【题目】在平面直角坐标系![]() 中,已知动点
中,已知动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 为定直线
为定直线![]() 上一点.
上一点.
①过点![]() 作
作![]() 的垂线交轨迹
的垂线交轨迹![]() 于点
于点![]() (
(![]() 不在
不在![]() 轴上),求证:直线
轴上),求证:直线![]() 与
与![]() 的斜率之积是定值;
的斜率之积是定值;
②若点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作动直线
作动直线![]() 交轨迹
交轨迹![]() 于不同两点
于不同两点![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,求证:点
,求证:点![]() 恒在一条定直线上.
恒在一条定直线上.
【答案】(1)![]() (2)①直线
(2)①直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
②点![]() 在定直线
在定直线![]() 上.
上.
【解析】试题分析:(1)设动点坐标![]() ,直接利用轨迹方程定义计算即可;(2)
,直接利用轨迹方程定义计算即可;(2)![]() ,
,
①令![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,即
,即![]() ,又因为点
,又因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,而
,而![]() 的斜率分别为
的斜率分别为![]() ,于是
,于是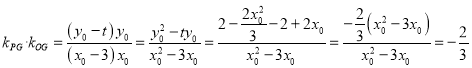 ,即直线
,即直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ; ②令
; ②令![]() ,则
,则![]() ,代入椭圆,消元即可证明点
,代入椭圆,消元即可证明点![]() 在定直线
在定直线![]() 上.
上.
试题解析:(1)设![]() ,则
,则![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由![]() ,得
,得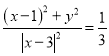 ,化简得
,化简得![]() ,
,
即点![]() 在轨迹
在轨迹![]() 的方程为
的方程为![]() ;
;
(2)因为![]() 为直线
为直线![]() 上一点,所以令
上一点,所以令![]() ,
,
①令![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,即
,即![]() ,
,
又因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
而![]() 的斜率分别为
的斜率分别为![]() ,
,
于是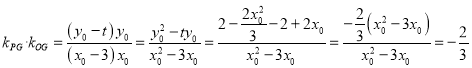 ,
,
即直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]()
.
②令![]() ,则
,则![]() ,
,
令点![]() ,则
,则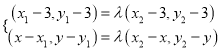 ,
,
即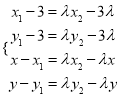 ,即
,即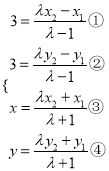
由①×③,②×④,得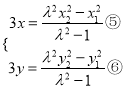 ,
,
因为![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
⑤×2+⑥×3,得![]()
![]() ,即
,即![]() ,
,
所以点![]() 在定直线
在定直线![]() 上.
上.
本题主要考查了椭圆的方程及直线与椭圆的位置关系,是高考的必考点,属于难题.求椭圆方程的方法一般就是根据条件建立![]() 的方程,求出
的方程,求出![]() 即可,注意
即可,注意![]() 的应用;涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出
的应用;涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出![]() ,再根据具体问题应用上式,其中要注意判别式条件的约束作用.
,再根据具体问题应用上式,其中要注意判别式条件的约束作用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目