题目内容
【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 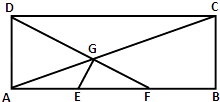
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F.
【答案】
(1)解:以A为原点,AB所在直线为x轴,建立平面直角坐标系,
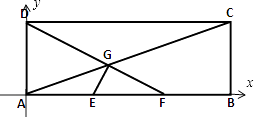
则A(0,0),B(3,0),C(3,1),D(0,1),E(1,0),F(2,0).
设M(x,y),由题意知|MD|=2|MC|
∴ ![]()
两边平方化简得:即(x﹣4)2+(y﹣1)2=4
即动点M的轨迹为圆心(4,1),半径为2的圆,
∴动点M的轨迹围成区域的面积为4π
(2)证明:由A(0,0).C(3,1)知直线AC的方程为:x﹣3y=0,
由D(0,1).F(2,0)知直线DF的方程为:x+2y﹣2=0,
由 ![]() 得
得 ![]() ,故点G点的坐标为
,故点G点的坐标为 ![]() .
.
又点E的坐标为(1,0),故kEG=2,kDF=﹣ ![]()
所以kEGkDF=﹣1,即证得:EG⊥DF
【解析】(1)以A为原点,AB所在直线为x轴,建立平面直角坐标系,求出动点M的轨迹方程,即可求出围成区域的面积;(2)求出直线AC,DF的方程,可得G的坐标,计算kEGkDF=﹣1,即可得到结论.

练习册系列答案
相关题目

