题目内容
如图,四棱锥P-ABCD的底面是矩形,侧面PAD
是正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.
(I)试判断直线PB与平面EAC的关系
(文科不必证明,理科必须证明);
(II)求证:AE⊥平面PCD;
(III)若AD=AB,试求二面角A-PC-D
的正切值.
是正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.
(I)试判断直线PB与平面EAC的关系
(文科不必证明,理科必须证明);

(II)求证:AE⊥平面PCD;
(III)若AD=AB,试求二面角A-PC-D
的正切值.
(I)PB∥平面EAC.(II)证明见解析 ,(III)二面角A-PC-D的正切值为 .
.
 .
. 解法一:
(I)PB∥平面EAC.证明如下:
连结BD交AC于点O,连结EO,则O为BD的中点,
又∵E为PD的中点,∴EO∥PB,∴PB∥平面EAC.
 (II)∵CD⊥AD,且侧面PAD⊥底面ABCD,
(II)∵CD⊥AD,且侧面PAD⊥底面ABCD,
而侧面PAD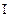 底面ABCD=AD,
底面ABCD=AD,
∴CD⊥侧面PAD,∴CD⊥AE.
∵侧面PAD是正三角形,E为侧棱PD的中点,
∴AE⊥PD,∴AE⊥平面PCD;
(III)过E作EM⊥PC于M,连结AM,由(2)及三垂线定理知AM⊥PC.
∴∠AME为二面角A-PC-D的平面角. 10分
由正三角形PAD及矩形ABCD,且AD=AB,∴PD=AD=AB=DC,
∴在等腰直角三角形DPC中,设AB=a,则AE= a,PC=
a,PC=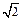 a,EM=
a,EM=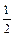 ×
× a. 12分
a. 12分
在 △AEM中,tan∠AME=
△AEM中,tan∠AME= =
= =
= .
.
即二面角A-PC-D的正切值为 .
.
解法二:(I)同解法一

(II)设N为AD中点,Q为BC中点,则因为△PAD是正三角形,底面ABCD是矩形,所以,PN⊥AD,QN⊥AD,又因为侧面PAD⊥底面ABCD,所以,PN⊥面ABCD,QN⊥面PAD,以N为坐标原点,NA、NQ、NP所在直线分别为x,y,z轴如图建立空间直角坐标系.设AD=1,AB=a,则 ,
,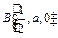 ,
,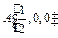 ,
,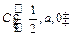 ,
, ,
, .
.
∴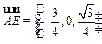 ,
, ,
,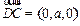 .
.
∴ ,
, .
.
∴ .又
.又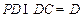 ,PD,DC
,PD,DC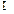 面PDC,
面PDC,
∴AE⊥平面PCD;
(III)当a=1时,由(2)可知: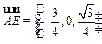 是平面PDC的法向量,
是平面PDC的法向量,
设平面PAC的法向量为 ,则
,则 ,
, ,
,
即 ,取x=1,可得:y=1,z=
,取x=1,可得:y=1,z=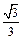 .所以,
.所以, .
.
向量 与
与 所成角
所成角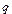 的余弦值为:
的余弦值为: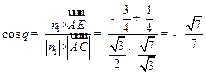 .
.
∴tanq= .
.
又由图可知,二面角A-PC-D的平面角为锐角,所以二面角A-PC-D的平面角就是向量 与
与 所成角
所成角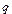 的补角.其正切值等于
的补角.其正切值等于 . 14分
. 14分
(I)PB∥平面EAC.证明如下:
连结BD交AC于点O,连结EO,则O为BD的中点,
又∵E为PD的中点,∴EO∥PB,∴PB∥平面EAC.
 (II)∵CD⊥AD,且侧面PAD⊥底面ABCD,
(II)∵CD⊥AD,且侧面PAD⊥底面ABCD,而侧面PAD
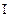 底面ABCD=AD,
底面ABCD=AD,∴CD⊥侧面PAD,∴CD⊥AE.
∵侧面PAD是正三角形,E为侧棱PD的中点,
∴AE⊥PD,∴AE⊥平面PCD;
(III)过E作EM⊥PC于M,连结AM,由(2)及三垂线定理知AM⊥PC.
∴∠AME为二面角A-PC-D的平面角. 10分
由正三角形PAD及矩形ABCD,且AD=AB,∴PD=AD=AB=DC,
∴在等腰直角三角形DPC中,设AB=a,则AE=
 a,PC=
a,PC=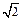 a,EM=
a,EM=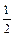 ×
× a. 12分
a. 12分在
 △AEM中,tan∠AME=
△AEM中,tan∠AME= =
= =
= .
. 即二面角A-PC-D的正切值为
 .
. 解法二:(I)同解法一

(II)设N为AD中点,Q为BC中点,则因为△PAD是正三角形,底面ABCD是矩形,所以,PN⊥AD,QN⊥AD,又因为侧面PAD⊥底面ABCD,所以,PN⊥面ABCD,QN⊥面PAD,以N为坐标原点,NA、NQ、NP所在直线分别为x,y,z轴如图建立空间直角坐标系.设AD=1,AB=a,则
 ,
,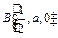 ,
,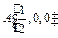 ,
,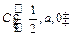 ,
, ,
, .
. ∴
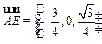 ,
, ,
,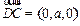 .
.∴
 ,
, .
.∴
 .又
.又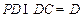 ,PD,DC
,PD,DC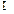 面PDC,
面PDC,∴AE⊥平面PCD;
(III)当a=1时,由(2)可知:
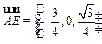 是平面PDC的法向量,
是平面PDC的法向量,设平面PAC的法向量为
 ,则
,则 ,
, ,
,即
 ,取x=1,可得:y=1,z=
,取x=1,可得:y=1,z=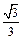 .所以,
.所以, .
. 向量
 与
与 所成角
所成角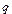 的余弦值为:
的余弦值为: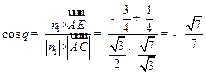 .
. ∴tanq=
 .
. 又由图可知,二面角A-PC-D的平面角为锐角,所以二面角A-PC-D的平面角就是向量
 与
与 所成角
所成角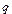 的补角.其正切值等于
的补角.其正切值等于 . 14分
. 14分
练习册系列答案
相关题目
 的值为多少时,
的值为多少时,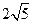 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交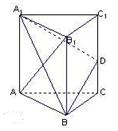
 如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.
如图,四棱柱ABCD—A1B1C1D1的底面边长和侧棱长都等于2,平面A1ACC1⊥平面ABCD,∠ABC=∠A1AC=60°,点O为底面对角线AC与BD的交点.

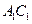
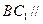 平面
平面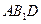
 的大小
的大小