题目内容
【题目】如图，在直角梯形
中，
，
，
，
，
，点
是线段
的中点，将
，
分别沿
，
向上折起，使
，
重合于点
，得到三棱锥
．试在三棱锥中，
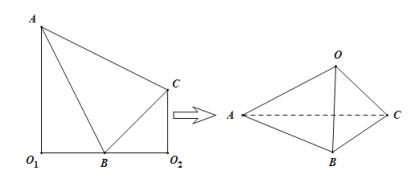
（1）证明：平面
平面
；
（2）求直线
与平面
所成角的正弦值．
【答案】（1）证明见解析；（2）
.
【解析】
（1）根据勾股定理的逆定理，得出
，而
，根据线面垂直的判定定理证出
平面
，最后利用面面垂直的判定定理，即可证明平面
平面；
（2）以
为坐标原点，
为
轴，
为
轴，
为
轴，建立空间直角坐标系，根据空间坐标的运算可得出
和平面
的法向量，利用空间向量法求夹角的公式，即可求出直线与平面所成角的正弦值．
解：（1）由题知：在直角梯形
中，
，
所以在三棱锥
中，
，
所以，
又因为，
，
所以平面， 又因为
平面
，
所以，平面平面.
（2）由（1）知：，，又
，
以为坐标原点，以
的方向分别作为轴，轴，轴的正方向，
建立如图空间直角坐标系
，
所以
，
，
，，
设
为平面的法向量，
，
，
由
，可得
，
令
得：
，
设直线与平面所成角为
，所以
，
所以直线与平面所成角的正弦值为.
练习册系列答案
相关题目
【题目】某地区对当地的某种土特产的销售量y（吨）和销售单价x（元/千克）之间的关系进行了调查，得到下表中的数据：
销售单价x（元/千克） | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y（吨） | 5 | 6 | 8 | 10 | 11 | 14.1 |
（1）根据前5组数据，求出y关于x的回归直线方程．
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5，则认为回归直线方程是理想的，试问（1）中得到的回归直线方程是否理想？
（3）如果销售量y（吨）和销售单价x（元/千克）之间仍然服从（1）中的关系，进货成本为2.5元/千克，且货源充足（未售完的部分可按成本价全部售出），为了使利润最大，请你就如何确定销售单价给出合理建议．（每千克销售单价不超过12元）
参考公式：回归直线方程
，其中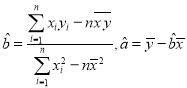
．
参考数据：
．
