Question

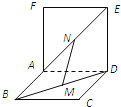
【题目】如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为（ ）
A.8+8 +4
B.8+8 +2
C.2+2 +
D. + +

Answer 1

【答案】A
【解析】解：由三视图可知几何体为从边长为4的正方体切出来的三棱锥A﹣BCD．作出直观图如图所示： 其中A，C，D为正方体的顶点，B为正方体棱的中点．
∴S△ABC= =4，S△BCD= =4．
∵AC=4 ，AC⊥CD，∴S△ACD= =8 ，
由勾股定理得AB=BD= =2 ，AD=4 ．
∴cos∠ABD= =﹣ ，∴sin∠ABD= ．
∴S△ABD= =4 ．
∴几何体的表面积为8+8 +4 ．
故选A．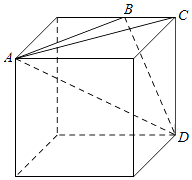

由三视图可知几何体为从边长为4的正方体切出来的三棱锥．作出直观图，计算各棱长求面积．