题目内容
【题目】已知a为实数,函数f(x)=x2﹣|x2﹣ax﹣2|在区间(﹣∞,﹣1)和(2,+∞)上单调递增,则a的取值范围为( )
A.[1,8]
B.[3,8]
C.[1,3]
D.[﹣1,8]
【答案】A
【解析】解:令函数g(x)=x2﹣ax﹣2,由于g(x)的判别式△=a2+8>0,故函数g(x)一定有两个零点, 设为x1 和x2 , 且 x1<x2 .
∵函数f(x)=x2﹣|x2﹣ax﹣2|= ![]() ,
,
故当x∈(﹣∞,x1)、(x2 , +∞)时,
函数f(x)的图象是位于同一条直线上的两条射线,
当x∈(x1 , x2 )时,函数f(x)的图象是抛物线y=2x2﹣ax﹣2下凹的一部分,且各段连在一起.
由于f(x)在区间(﹣∞,﹣1)和(2,+∞)上单调递增,
∴a>0且函数g(x)较小的零点x1= ![]() ≥﹣1,
≥﹣1,
即a+2≥ ![]() ,
,
平方得a2+4a+4≥a2+8,得a≥1,
同时由y=2x2﹣ax﹣2的对称轴为x= ![]() ,
,
若0≤ ![]() ≤2,可得0≤a≤8.
≤2,可得0≤a≤8.
综上可得,1≤a≤8,
故实a的取值范围为[1,8],
故选:A.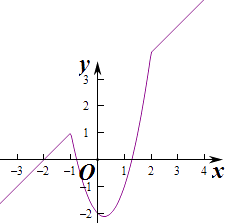
【考点精析】本题主要考查了函数单调性的性质的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.

【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了![]() 名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
(2)若参赛选手共![]() 万人,用频率估计概率,试估计其中优秀等级的选手人数;
万人,用频率估计概率,试估计其中优秀等级的选手人数;
【题目】为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:
![]()
(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断:![]() 与y=
与y=![]() 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
|
|
|
|
|
|
3.5 | 62.83 | 3.53 | 17.5 | 596.505 | 12.04 |
其中![]() ;
;![]()
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 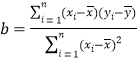
![]()

