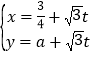题目内容
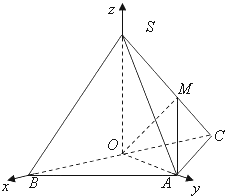
【题目】如图,在三棱锥S﹣ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. (Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A﹣SC﹣B的余弦值.
【答案】证明: (Ⅰ)由题设AB=AC=SB=SC=SA,连接OA,△ABC为等腰直角三角形,
所以 ![]() ,且AO⊥BC,
,且AO⊥BC,
又△SBC为等腰三角形,故SO⊥BC,
且 ![]() ,从而OA2+SO2=SA2 .
,从而OA2+SO2=SA2 .
所以△SOA为直角三角形,SO⊥AO.
又AO∩BO=O.
所以SO⊥平面ABC.
(Ⅱ)解:
以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,
建立如图的空间直角坐标系O﹣xyz.
设B(1,0,0),则C(﹣1,0,0),A(0,1,0),S(0,0,1).SC的中点 ![]() ,
, ![]() .
.
∴ ![]() .
.
故 ![]() 等于二面角A﹣SC﹣B的平面角.
等于二面角A﹣SC﹣B的平面角.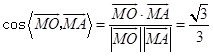 ,
,
所以二面角A﹣SC﹣B的余弦值为 ![]() .
.
【解析】(1)欲证SO⊥平面ABC,根据直线与平面垂直的判定定理可知只需证SO与平面ABC内两相交直线垂直,而SO⊥BC,SO⊥AO,又AO∩BO=O,满足定理条件;(2)以O为坐标原点,射线OB,OA分别为x轴、y轴的正半轴,建立空间直角坐标系O﹣xyz,求出两半平面的法向量,求出两法向量的夹角即可.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).

练习册系列答案
相关题目