题目内容

4．设a＞0且a≠1．则“函数f（x）=logax是（0，+∞）上的增函数”是“函数g（x）=（1-a）•ax”是R上的减函数的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 根据充分条件和必要条件的定义结合函数单调性的性质进行判断即可．

解答 解：函数f（x）=logax是（0，+∞）上的增函数，则a＞1，
若“函数g（x）=（1-a）•ax”是R上的减函数，则$\left\{\begin{array}{l}{a＞1}\\{1-a＜0}\end{array}\right.$或$\left\{\begin{array}{l}{0＜a＜1}\\{1-a＞0}\end{array}\right.$，即a＞1或0＜a＜1，
故“函数f（x）=logax是（0，+∞）上的增函数”是“函数g（x）=（1-a）•ax”是R上的减函数的充分不必要条件，
故选：A

点评 本题主要考查充分条件和必要条件的判断，根据函数的单调性求出等价条件是解决本题的关键．

练习册系列答案
相关题目
14．函数f（x）=x3-$\frac{a}{2}$x2-2a2x+$\frac{3}{2}$的图象经过四个象限，则a的取值范围是（-∞，-$\frac{9\sqrt{11}}{22}$）∪（1，+∞）．
15．已知直线l：2x-y=3，若矩阵A=$（\begin{array}{l}{-1}&{a}\\{b}&{3}\end{array}）$a，b∈R所对应的变换σ把直线l变换为它自身．
（Ⅰ）求矩阵A；                  
（Ⅱ）求矩阵A的逆矩阵．
12．已知集合M={x|-1＜x＜1}，N={x|x（x-2）＜0}，则M∩N为（　　）
A．（-1，2）B．（0，1）C．（-1，0）D．（-1，1）
19．从集合{2，3，4，5}中随机抽取一个数a，从集合{1，3，5}中随机抽取一个数b，则向量$\overrightarrow{m}$=（a，b）与向量$\overrightarrow{n}$=（-1，1）垂直的概率为$\frac{1}{6}$．
9．已知等差数列{an}的公差为d（d≠0），等比数列{bn}的公比为q（q＞0），且满足a1=b1=1，a2=b3，a6=b
5
（1）求数列{an}的通项公式；
（2）数列{bn}的前n项和为Tn，求证：$\frac{1}{{T}_{1}}$+$\frac{1}{{T}_{2}}$+…+$\frac{1}{{T}_{n}}$＜2．
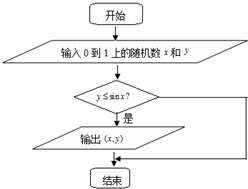16．由计算机产生的两个0到1上的随机数，按右侧流程图所示的规则，则能输出数对（x，y）的概率是1-cos1．
13．已知实数x，y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ 3x-y-3≤0\end{array}\right.$，则当2x-y取得最小值时，x2+y2的值为5．
14．已知函数f（x）=$\frac{x}{lnx}$-ax（a＞0，a≠1）
（1）若函数f（x）在[e，e2]上为单调增函数，求实数a的取值范围；
（2）若?x1，x2∈[e，e2]，使f（x1）≤f'（x2）+a成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网