题目内容
13.已知实数x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ 3x-y-3≤0\end{array}\right.$,则当2x-y取得最小值时,x2+y2的值为5.分析 先画出满足条件的平面区域,求出2x-y取得最小值时A点的坐标,将A点的坐标代入x2+y2,求出即可.
解答 解:画出满足条件的平面区域,如图,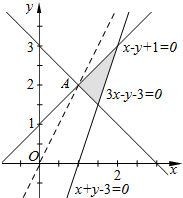 ,
,
令z=2x-y,
则当直线z=2x-y经过直线x-y+1=0和直线
x+y-3=0的交点A时,z取得最小值.
此时A的坐标为(1,2),
∴x2+y2=5,
故答案为:5.
点评 本题考察了简单的线性规划问题,考察数形结合思想,求出2x-y取得最小值时的x,y的值是解题的关键,本题是一道中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
4.设a>0且a≠1.则“函数f(x)=logax是(0,+∞)上的增函数”是“函数g(x)=(1-a)•ax”是R上的减函数的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.已知$\frac{m}{1+i}$=1-ni,其中m,n是实数,i是虚数单位,则m+n=( )
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
2.若p:0<x<2是q:a-1<x≤a的必要不充分条件,则a的取值范围是( )
| A. | [1,2] | B. | [1,2) | C. | [1,2) | D. | (1,2] |
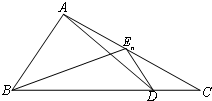 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中