题目内容
已知等比数列{an}的前n项和Sn=2n-a,n∈N*.设公差不为零的等差数列{bn}满足:b1=a1+2,且b2+5,b4+5,b8+5成等比数列.
(Ⅰ)求a的值及数列{bn}的通项公式;
(Ⅱ)设数列{log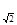 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.
(Ⅰ)a=1,bn=8n-5;(Ⅱ)9.
解析试题分析:(Ⅰ)依据Sn=2n-a,根据数列的前n项和,求出数列{an}的通项公式,并且根据初始条件求出a=1,an=2n-1,再根据b2+5,b4+5,b8+5成等比数列,得出(b4+5)2=(b2+5)(b8+5),解得d=0(舍去),或d=8,从而求出{bn}的通项公式为bn=8n-5;(Ⅱ)由(Ⅰ)an=2n-1代入log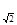 an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=
an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=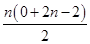 =n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
=n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
试题解析:
(Ⅰ)当n=1时,a1=S1=2-a;
当n≥2时,an=Sn-Sn-1=2n-1.
∵{an}为等比数列,
∴2-a=1,解得a=1.
∴an=2n-1.
设数列{bn}的公差为d,
∵b2+5,b4+5,b8+5成等比数列,
∴(b4+5)2=(b2+5)(b8+5),
又b1=3,
∴(8+3d)2=(8+d)(8+7d),
解得d=0(舍去),或d=8.
∴bn=8n-5.
(Ⅱ)由an=2n-1,得log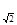 an=2(n-1),
an=2(n-1),
∴{log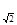 an}是以0为首项,2为公差的等差数列,
an}是以0为首项,2为公差的等差数列,
∴Tn=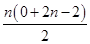 =n(n-1).
=n(n-1).
由bn=8n-5,Tn>bn,得
n(n-1)>8n-5,即n2-9n+5>0,
∵n∈N*,∴n≥9.
故所求n的最小正整数为9.
考点:1.数列通项公式的求解;2.等差、等比数列的性质应用.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案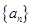 是首项为
是首项为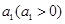 ,公差为
,公差为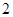 的等差数列,其前
的等差数列,其前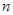 项和为
项和为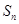 ,且
,且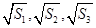 成等差数列.
成等差数列.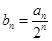 的前
的前 ,求
,求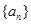 ,公差
,公差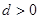 ,前n项和为
,前n项和为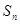 ,
,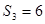 ,且满足
,且满足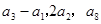 成等比数列.
成等比数列.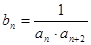 ,求数列
,求数列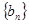 的前
的前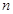 项和
项和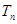 的值.
的值.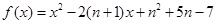 .
.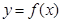 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列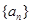 ,求证:
,求证: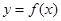 的图像的顶点到
的图像的顶点到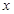 轴的距离构成数列
轴的距离构成数列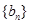 ,求
,求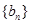 的前
的前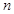 项和
项和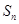 .
.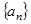 的各项均是正数,其前
的各项均是正数,其前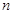 项和为
项和为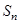 ,满足
,满足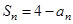 .
.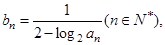 数列
数列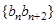 的前
的前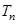 ,求证:
,求证: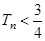 .
. 的首项
的首项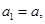 其中
其中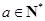 ,
,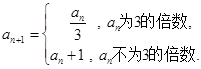 令集合
令集合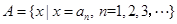 .
.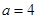 ,写出集合
,写出集合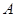 中的所有的元素;
中的所有的元素;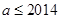 ,且数列
,且数列 的所有可能取值构成的集合;
的所有可能取值构成的集合;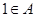 .
.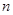 年该生产线设备低劣化值为
年该生产线设备低劣化值为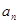 ,求
,求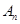 ,当
,当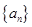 满足:
满足: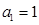 ,
,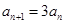 ,
,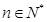 .
. 项和
项和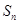 ;
;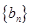 是等差数列,
是等差数列,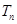 为前
为前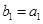 ,
,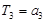 .求
.求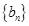 的通项公式,并证明:
的通项公式,并证明: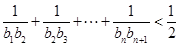 .
.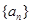 满足
满足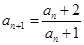 ,且
,且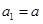 ,
,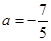 时,求出数列
时,求出数列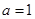 时,设
时,设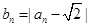 ,证明:
,证明: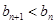 ;
;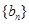 的前
的前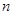 项和为
项和为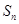 ,证明:
,证明: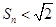 .
.