题目内容
设数列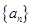 是首项为
是首项为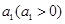 ,公差为
,公差为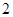 的等差数列,其前
的等差数列,其前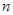 项和为
项和为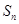 ,且
,且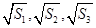 成等差数列.
成等差数列.
(1)求数列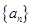 的通项公式;
的通项公式;
(2)记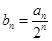 的前
的前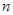 项和为
项和为 ,求
,求 .
.
(1) (2)
(2)
解析试题分析:(1)由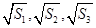 成等差数列得,
成等差数列得,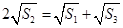 ,可解得
,可解得 ,用等差的通项公式可得
,用等差的通项公式可得 。(2)因为
。(2)因为 等于等差成等比的形式,所以求其前
等于等差成等比的形式,所以求其前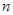 项和应用错位相减法,即写出
项和应用错位相减法,即写出 的式子后,将式子两边同乘以通项公式中的等比数列的公比即可,但须往后错一位写出其式子,然后两式相减计算即可。
的式子后,将式子两边同乘以通项公式中的等比数列的公比即可,但须往后错一位写出其式子,然后两式相减计算即可。
试题解析:解:(1)∵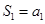 ,
, ,
,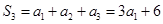 , 2分
, 2分
由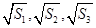 成等差数列得,
成等差数列得,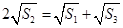 ,
,
即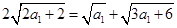 , 3分
, 3分
解得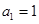 ,故
,故 ; 6分
; 6分
(2)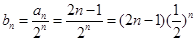 ,
,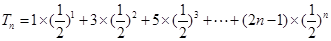 , ① ①
, ① ① 得,
得, ② 8分
② 8分
① ②得,
②得,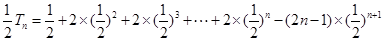
 10分
10分
∴ . 12分
. 12分
考点:1等差中项;2等差的通项公式;3错位相减法求数列的前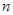 项和。
项和。

练习册系列答案
相关题目
 的前n项和记为
的前n项和记为 ,点(n,
,点(n,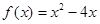 (
(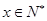 )上
)上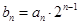 ,求数列
,求数列 的前n项和
的前n项和 的值.
的值. 的前
的前 项和为
项和为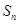 ,
,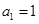 ,
,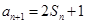 ,等差数列
,等差数列 满足
满足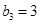 ,
,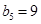 .
.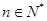 ,不等式
,不等式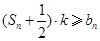 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.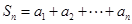 ,
, ,且
,且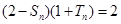 ,
, .
.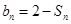 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;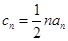 ,求集合
,求集合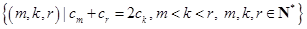 .
.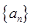 满足:
满足: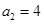 ,且对于任何
,且对于任何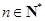 ,有
,有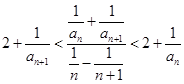 .
.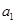 ,
,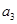 ;
;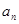 .
.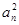 ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn..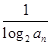 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得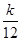 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.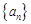 的前
的前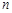 项和
项和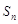 满足
满足 ,又
,又 ,
,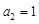 .
. an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.