题目内容
某企业为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的设备维修、燃料和动力等消耗的费用(称为设备的低劣化值)会逐年增加,第一年设备低劣化值是4万元,从第二年到第七年,每年设备低劣化值均比上年增加2万元,从第八年开始,每年设备低劣化值比上年增加25%.
(1)设第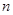 年该生产线设备低劣化值为
年该生产线设备低劣化值为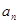 ,求
,求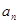 的表达式;
的表达式;
(2)若该生产线前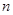 年设备低劣化平均值为
年设备低劣化平均值为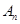 ,当
,当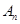 达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
(1) ;(2)第九年.
;(2)第九年.
解析试题分析:(1)可知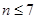 时,
时,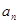 构成等差数列;
构成等差数列;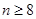 时
时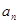 构成等比数列.然后由条件即可得出
构成等比数列.然后由条件即可得出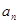 的表达式,注意写出分段函数的形式;(2)先写出
的表达式,注意写出分段函数的形式;(2)先写出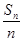 即
即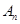 的表达式,然后判定其单调性,得出
的表达式,然后判定其单调性,得出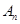 是增函数,从而求出
是增函数,从而求出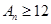 时
时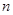 的取值范围.所以得到第九年需要更新该生产线.
的取值范围.所以得到第九年需要更新该生产线.
试题解析:(1)当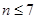 时,数列
时,数列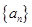 是首项为4,公差为2的等差数列,
是首项为4,公差为2的等差数列,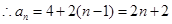 3分
3分
当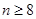 时,数列
时,数列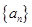 是首项为
是首项为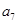 ,公比为
,公比为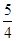 的等比数列,又
的等比数列,又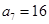 ,
,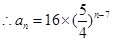
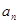 的表达式为
的表达式为 6分
6分
(2)设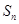 表示数列
表示数列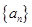 的前
的前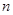 项和,由等差及等比数列的求和公式得
项和,由等差及等比数列的求和公式得
当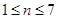 时,
时,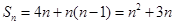
当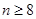 时,由
时,由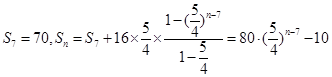
该生产线前n年设备低劣化平均值为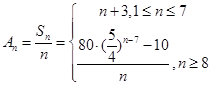 9分
9分
当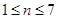 时,数列
时,数列 为单调递增数列;
为单调递增数列;
当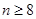 时,
时,
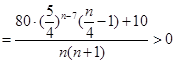 ,
,
所以 为单调递增数列. 11分
为单调递增数列. 11分
又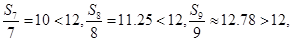 则第九年需要更新该生产线. 13分
则第九年需要更新该生产线. 13分
考点:1.等差及等比数列的通项公式;2.等差及等比数列的求和公式;3.数列的单调性.

练习册系列答案
相关题目
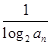 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得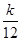 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.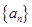 中,
中,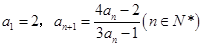 ,设
,设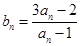 .
.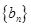 的前三项;
的前三项;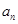 ;
;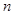 项和为
项和为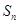 ,
,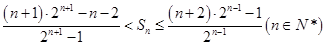 .
.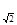 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.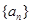 的前
的前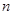 项和为
项和为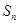 ,常数
,常数 ,且
,且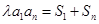 对一切正整数
对一切正整数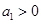 ,
,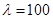 ,当
,当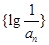 的前
的前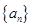 中,
中,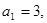
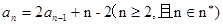
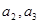 的值;
的值;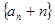 是等比数列,并求
是等比数列,并求 .
.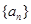 的所有项均为正数,首项
的所有项均为正数,首项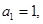 且
且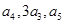 成等差数列.
成等差数列.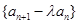 的前
的前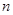 项和为
项和为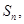 若
若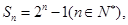 求实数
求实数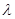 的值.
的值.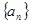 的前n项和为
的前n项和为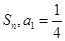 且
且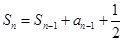 ,数列
,数列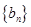 满足
满足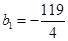 且
且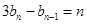
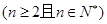 .
.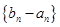 为等比数列;
为等比数列;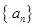 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称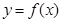 使得
使得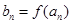 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称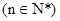 .
.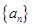 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若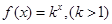 是数列
是数列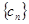 的首项为2010,
的首项为2010, 是数列
是数列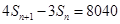 ,证明
,证明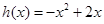 ,
,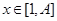 ,和数列1,
,和数列1,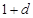 ,
,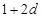 ,(
,(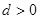 )提出一个正确的命题,并说明理由.
)提出一个正确的命题,并说明理由.