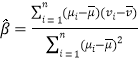题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)求![]() 在
在![]() 上的单调性及极值;
上的单调性及极值;
(2)若![]() ,对任意的
,对任意的![]() ,不等式
,不等式![]() 都在
都在![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 递减,
递减, ![]() 递增,极小值
递增,极小值![]() ,无极大值;(2)
,无极大值;(2)![]() .
.
【解析】试题分析:(1)第(1)问,直接利用求导求函数的单调性和极值. (2)转化成证明g(x)的最大值小于零,在![]() 上,
上, ![]() 有解,再证明
有解,再证明![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
令![]() ,∴
,∴![]()
∴![]() 在
在![]() 递减,
递减, ![]() 递增,
递增,
∴极小值![]() ,无极大值.
,无极大值.
(2)因为![]() ,令
,令![]() ,
, ![]() ,
,
则![]() 为关于
为关于![]() 的一次函数且为减函数,
的一次函数且为减函数,
根据题意,对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,
成立,
则在![]() 上,
上, ![]() 有解,
有解,
令![]() ,只需存在
,只需存在![]() 使得
使得![]() 即可,
即可,
由于![]() ,
,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,不符合题意.
,不符合题意.
②当![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() ,
,
若![]() ,则
,则![]() ,所以在
,所以在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.
,符合题意.
若![]() ,则
,则![]() ,∴在
,∴在![]() 上一定存在实数
上一定存在实数![]() ,使得
,使得![]() ,
,
∴在![]() 上
上![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴存在![]() 使得
使得![]() ,符合题意.
,符合题意.
综上所述,当![]() 时,对任意的
时,对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立.
成立.

【题目】现有某高新技术企业年研发费用投入![]() (百万元)与企业年利润
(百万元)与企业年利润![]() (百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
(百万元)之间具有线性相关关系,近5年的年研发费用和年利润的具体数据如表:
年研发费用 |
|
|
|
|
|
年利润 |
|
|
|
|
|
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(1)求![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)如果该企业某年研发费用投入8百万元,预测该企业获得年利润为多少?
参考数据:回归直线的系数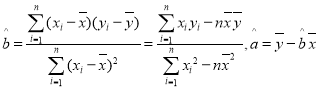 .
.
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列2×2列联表,并回答能否有90%的把握认为年龄层与热衷关心民生大事有关?

(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?

![]() .
.
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()