题目内容
【题目】定圆M： 
=16，动圆N过点F 
且与圆M相切，记圆心N的轨迹为E．
（I）求轨迹E的方程；
（Ⅱ）设点A，B，C在E上运动，A与B关于原点对称，且|AC|=|CB|，当△ABC的面积最小时，求直线AB的方程．
【答案】解：（Ⅰ）因为点 
在圆 
内，所以圆N内切于圆M，因为|NM|+|NF|=4＞|FM|，所以点N的轨迹E为椭圆，且 
，所以b=1，所以轨迹E的方程为 
．
（Ⅱ）（i）当AB为长轴（或短轴）时，依题意知，点C就是椭圆的上下顶点（或左右顶点），
此、时 
|AB|=2．
（ii）当直线AB的斜率存在且不为0时，设其斜率为k，直线AB的方程为y=kx，
联立方程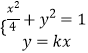 
得 
，
所以|OA|2= 
．
由|AC|=|CB|知，△ABC为等腰三角形，O为AB的中点，OC⊥AB，所以直线OC的方程为 
，
由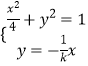 
解得 
， 
= 
， 
，
S△ABC=2S△OAC=|OA|×|OC|= 
，
由于 
，所以 
，
当且仅当1+4k2=k2+4，即k=±1时等号成立，此时△ABC面积的最小值是 
，
因为 
，所以△ABC面积的最小值为 ，此时直线AB的方程为y=x或y=﹣x．
【解析】（Ⅰ）根据点的几何意义|NM|+|NF|=4＞|FM|，可得点N的轨迹E为椭圆，由已知可求出方程。
（Ⅱ）分情况讨论（i）当直线AB的斜率不存在时，AB为长轴（或短轴）时，依题意知，点C就是椭圆的上下顶点，即可求出面积。
（ii）当直线AB的斜率存在且不为0时，设其斜率为k，直线AB的方程为y=kx， ，联立直线与椭圆的方程，求出|OA|2的关于k的代数式，由已知可得OC⊥AB，可设直线OC的方程为 y = 
x ,联立直线与椭圆的方程可得到 | O C |2的关于k的代数式，再根据三角形的面积公式S△ABC=2S△OAC=|OA|×|OC|利用基本不等式可得出最小值，当且仅当1+4k2=k2+4，即k=±1时等号成立，故得直线AB的方程为y=x或y=﹣x．
