题目内容
【题目】已知椭圆Γ: ![]() =1(a>b>0)的右焦点为(2
=1(a>b>0)的右焦点为(2 ![]() ,0),且椭圆Γ上一点M到其两焦点F1 , F2的距离之和为4
,0),且椭圆Γ上一点M到其两焦点F1 , F2的距离之和为4 ![]() .
.
(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆Γ交于不同两点A,B,且|AB|=3 ![]() .若点P(x0 , 2)满足|
.若点P(x0 , 2)满足| ![]() |=|
|=| ![]() |,求x0的值.
|,求x0的值.
【答案】解:(Ⅰ)由已知2a=4 ![]() ,得a=2
,得a=2 ![]() ,又c=2
,又c=2 ![]() . ∴b2=a2﹣c2=4.
. ∴b2=a2﹣c2=4.
∴椭圆Γ的方程为 ![]() .
.
(Ⅱ)由 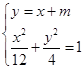 ,得4x2+6mx+3m2﹣12=0,①
,得4x2+6mx+3m2﹣12=0,①
∵直线l与椭圆Γ交于不同两点A、B,
∴△=36m2﹣16(3m2﹣12)>0,
解得m2<16.
设A(x1 , y1),B(x2 , y2),则x1 , x2是方程①的两根,
则 ![]() ,
, ![]() .
.
∴|AB|= ![]() =
= ![]() =
= ![]() .
.
又由|AB|=3 ![]() ,得﹣
,得﹣ ![]() ,解得m=±2
,解得m=±2
据题意知,点P为线段AB的中垂线与直线y=2的交点.
设AB的中点为E(x0 , y0),则 ![]() =﹣
=﹣ ![]() ,
, ![]() ,
,
当m=2时,E(﹣ ![]() ),
),
∴此时,线段AB的中垂线方程为y﹣ ![]() =﹣(x+
=﹣(x+ ![]() ),即y=﹣x﹣1.
),即y=﹣x﹣1.
令y=2,得x0=﹣3.
当m=﹣2时,E( ![]() ),
),
∴此时,线段AB的中垂线方程为y+ ![]() =﹣(x﹣
=﹣(x﹣ ![]() ),即y=﹣x+1.
),即y=﹣x+1.
令y=2,得x0=﹣1.…(1分)
综上所述,x0的值为﹣3或﹣1
【解析】(Ⅰ)由已知2a=4 ![]() ,c=2
,c=2 ![]() .由此能求出椭圆Γ的方程.(Ⅱ)由
.由此能求出椭圆Γ的方程.(Ⅱ)由  ,得4x2+6mx+3m2﹣12=0,由此利用根的判别式、韦达定理、中垂线性质、中点坐标公式,结合已知条件能求出x0的值.
,得4x2+6mx+3m2﹣12=0,由此利用根的判别式、韦达定理、中垂线性质、中点坐标公式,结合已知条件能求出x0的值.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目