题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)求S1 , S2 , S3 , S4并猜想Sn的表达式(不必写出证明过程);
(2)设bn= ![]() ,n∈N*,求bn的最大值.
,n∈N*,求bn的最大值.
【答案】
(1)解:∵a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).∴
,2Sn﹣SnSn﹣1=1(n≥2).∴ ![]() =1,解得S2=
=1,解得S2= ![]() .
.
同理可得:S3= ![]() ,S4=
,S4= ![]() .
.
猜想Sn= ![]()
(2)解:由(1)可得:n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =
= ![]() .
.
bn= ![]() =
= 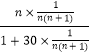 =
= ![]() =
= ![]() ≤
≤ ![]() ,n∈N*,
,n∈N*,
b5= ![]() ,b6=
,b6= ![]() .
.
∴bn的最大值为 ![]()
【解析】(1)a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).可得
,2Sn﹣SnSn﹣1=1(n≥2).可得 ![]() =1,解得S2 . 同理可得:S3 , S4 . 猜想Sn=
=1,解得S2 . 同理可得:S3 , S4 . 猜想Sn= ![]() .(2)由(1)可得:n≥2时,an=Sn﹣Sn﹣1=
.(2)由(1)可得:n≥2时,an=Sn﹣Sn﹣1= ![]() .可得bn=
.可得bn= ![]() =
= ![]() ,利用基本不等式的性质、函数的单调性即可得出.
,利用基本不等式的性质、函数的单调性即可得出.
【考点精析】本题主要考查了数列的前n项和和归纳推理的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系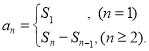 ;根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理才能正确解答此题.
;根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理才能正确解答此题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目