题目内容
【题目】某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组
，第2组
，第3组
，第4组
，第5组
，得到的频率分布图如图所示，下表是年龄的频率分布表.
（1）现要从年龄较小的第
组中用分层抽样的方法抽取6人，则年龄第组人数分别是多少？
（2）在（1）的条件下，从这6中随机抽取2参加社区宣传交流活动，求恰有2人在第3组的概率。
【答案】（1）年龄第1，2，3组人数分别是1人，1人，4人；（2）
.
【解析】试题分析：（1）由频率分布表和频率分布直方图知第1，2，3组的人数比为
，要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，由此能求出年龄第1，2，3组人数．
（2）从这6人中随机抽取2人参加社区宣传交流活动，基本事件总数
种，恰有2人在第3组包含的基本事件个数
种，由此能求出恰有2人在第3组的概率．
试题解析：（1）由频率分布表和频率分布直方图知：
第1组[25，30）的频率为0.02×5=0.1，
第2组[30，35）的频率为0.02×5=0.1，
第3组[35，40）的频率为0.08×5=0.4，
第1，2，3组的人数比为0.1：0.1：0.4=1：1：4，
要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，
则年龄第1，2，3组人数分别是1人，1人，4人．
（2）从这6人中随机抽取2人参加社区宣传交流活动，
基本事件总数种，
恰有2人在第3组包含的基本事件个数种，
∴恰有2人在第3组的概率
．
【题目】给出最小二乘法下的回归直线方程 
= 
x+ 
系数公式： = 
， 
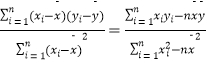假设关于某设备的使用年限x（年）和所支出的维修费用y（万元），有如表的统计资料：
使用年限x （年） | 2 | 3 | 4 | 5 | 6 |
维修费用y（万元） | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系，试求：
（1）线性回归直线方程；
（2）根据回归直线方程，估计使用年限为12年时，维修费用是多少？
