题目内容
已知椭圆 过点
过点 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2) 为椭圆
为椭圆 的左右顶点,直线
的左右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线 于
于 两点.证明:当点
两点.证明:当点 在椭圆
在椭圆 上运动时,
上运动时, 恒为定值.
恒为定值.
 过点
过点 ,且离心率为
,且离心率为 .
.(1)求椭圆
 的方程;
的方程;(2)
 为椭圆
为椭圆 的左右顶点,直线
的左右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线 于
于 两点.证明:当点
两点.证明:当点 在椭圆
在椭圆 上运动时,
上运动时, 恒为定值.
恒为定值.解:(1)由题意可知, 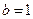 , 而
, 而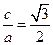 , 且
, 且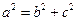 . 解得
. 解得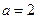 ,
,
所以,椭圆的方程为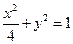 .
.
(2)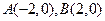 .设
.设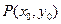 ,
,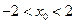 ,
,
……………6分
直线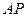 的方程为
的方程为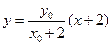 ,令
,令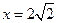 ,则
,则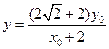 ,
,
即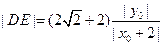 ;
;
直线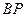 的方程为
的方程为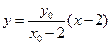 ,令
,令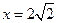 ,则
,则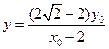 ,
,
即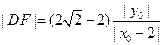 ;
;
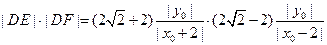
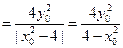
而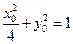 ,即
,即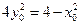 ,代入上式,
,代入上式,
∴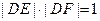 , 所以
, 所以 为定值
为定值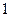
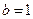 , 而
, 而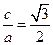 , 且
, 且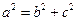 . 解得
. 解得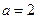 ,
,所以,椭圆的方程为
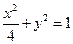 .
. (2)
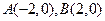 .设
.设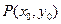 ,
,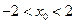 ,
, ……………6分
直线
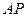 的方程为
的方程为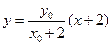 ,令
,令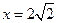 ,则
,则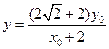 ,
,即
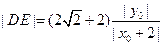 ;
; 直线
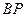 的方程为
的方程为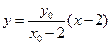 ,令
,令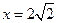 ,则
,则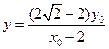 ,
,即
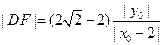 ;
; 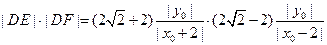
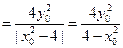
而
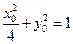 ,即
,即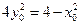 ,代入上式,
,代入上式,∴
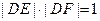 , 所以
, 所以 为定值
为定值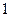
略

练习册系列答案
相关题目
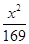 +
+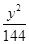 =1上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
=1上一点,F1、F2是椭圆的焦点,若|PF1|等于4,则|PF2|等于( )
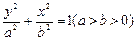 经过点
经过点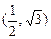 ,一个焦点是
,一个焦点是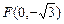 .
.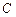 的方程;
的方程;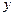 轴的两个交点为
轴的两个交点为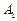 、
、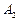 ,点
,点 在直线
在直线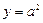 上,直线
上,直线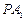 、
、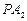 分别与椭圆
分别与椭圆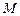 、
、 两点.试问:当点
两点.试问:当点 是否恒经过定点
是否恒经过定点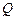 ?证明你的结论.
?证明你的结论.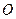 为坐标原点,
为坐标原点,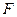 为椭圆
为椭圆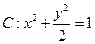 在
在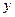 轴正半轴上的焦点,过
轴正半轴上的焦点,过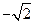 的直线
的直线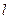 与
与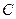 交与
交与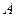 、
、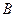 两点,点
两点,点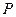 满足
满足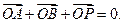
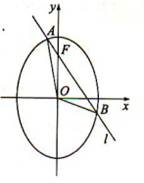
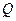 ,证明:
,证明: )作直线交椭圆
)作直线交椭圆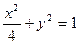 于A,B两点,若
于A,B两点,若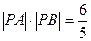 ,求直线
,求直线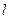 的方程。
的方程。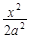 +
+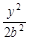 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线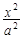 -
-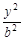 =1有相同的焦点,则椭圆的离心率为
=1有相同的焦点,则椭圆的离心率为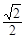

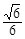
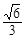
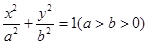 与双曲线
与双曲线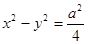 有相同的焦点,则椭圆的离心率为 ( )
有相同的焦点,则椭圆的离心率为 ( )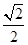
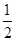
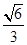

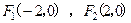 ,则这个椭圆的离心率等于_________________:
,则这个椭圆的离心率等于_________________: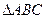 中,∠ABC=450,∠ACB=600,
中,∠ABC=450,∠ACB=600, ,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条
,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条