题目内容
(本大题共12分)
过点P(1,0 )作直线交椭圆
)作直线交椭圆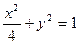 于A,B两点,若
于A,B两点,若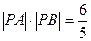 ,求直线
,求直线 的方程。
的方程。
过点P(1,0
 )作直线交椭圆
)作直线交椭圆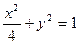 于A,B两点,若
于A,B两点,若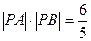 ,求直线
,求直线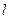 的方程。
的方程。解:设直线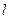 的方
的方 程是
程是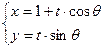 (
(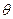 为参数)
为参数)
代入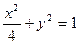 得
得 :
: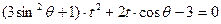
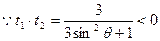
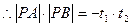
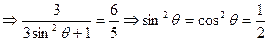
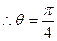 或
或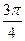 所求的直线
所求的直线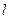 的方程是
的方程是 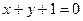 或
或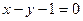
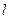 的方
的方 程是
程是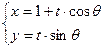 (
(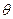 为参数)
为参数)代入
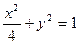 得
得 :
: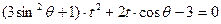
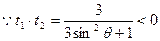
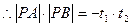
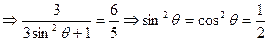
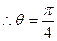 或
或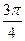 所求的直线
所求的直线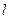 的方程是
的方程是 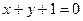 或
或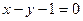
略

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
题目内容
 )作直线交椭圆
)作直线交椭圆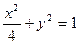 于A,B两点,若
于A,B两点,若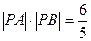 ,求直线
,求直线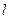 的方程。
的方程。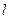 的方
的方 程是
程是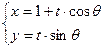 (
(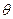 为参数)
为参数)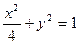 得
得 :
: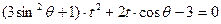
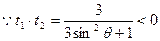
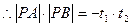
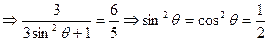
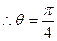 或
或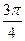 所求的直线
所求的直线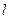 的方程是
的方程是 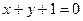 或
或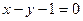

 快捷英语周周练系列答案
快捷英语周周练系列答案