题目内容
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界. 已知函数f(x)=1+a( ![]() )x+(
)x+( ![]() )x;g(x)=
)x;g(x)= ![]()
(Ⅰ)当a=1时,求函数f(x)值域并说明函数f(x)在(﹣∞,0)上是否为有界函数?
(Ⅱ)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围;
(Ⅲ)已知m>﹣1,函数g(x)在[0,1]上的上界是T(m),求T(m)的取值范围.
【答案】解:(Ⅰ)∵f(x)=1+a( ![]() )x+(
)x+( ![]() )x , ∴当a=1时,
)x , ∴当a=1时, ![]() ,
,
∵y= ![]() 和y=
和y= ![]() 在R上是单调递减函数,
在R上是单调递减函数,
∴f(x)在R上是单调递减函数,
∴f(x)在(﹣∞,0)上是单调递减函数,
∴f(x)>f(0)=3,
∴f(x)在(﹣∞,0)的值域为(3,+∞),
∴|f(x)|>3,
故不存在常数M>0,使|f(x)|≤M成立,
∴函数f(x)在(﹣∞,0)上不是有界函数;
(Ⅱ)∵函数f(x)在[0,+∞)上是以3为上界的有界函数,
∴由题意知,|f(x)|≤3在[0,+∞)上恒成立,
∴﹣3≤f(x)≤3在[1,+∞)上恒成立,
∴ ![]() 在[0,+∞)上恒成立,
在[0,+∞)上恒成立,
∴ ![]() 在[0,+∞)上恒成立,
在[0,+∞)上恒成立,
∴ 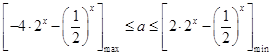 ,
,
令t=2x , 由x∈[0,+∞),可得t≥1,
∴ ![]() ,
, ![]() ,
,
下面判断函数h(t)和p(t)的单调性:
设1≤t1<t2 , 则t2﹣t1>0,4t1t2﹣1>0,t1t2>0,2t1t2+1>0,
∴ ![]() ,
,![]() ,
,
∴h(t1)>h(t2),p(t1)<p(t2),
∴h(t)在[1,+∞)上递减,p(t)在[1,+∞)上递增
∴h(t)在[1,+∞)上的最大值为h(1)=﹣5,
p(t)在[1,+∞)上的最小值为p(1)=1,
∴﹣5≤a≤1,
∴实数a的取值范围为[﹣5,1];
(Ⅲ)g(x)= ![]() =﹣1+
=﹣1+ ![]() ,
,
①当m>0时,x∈[0,1],
∵y=mx2+1在[0,1]上单调递增,
∴g(x)在[0,1]上递减,
∴g(1)≤g(x)≤g(0),即 ![]() ,
,
∵ ![]() ,
,
∴|g(x)|<1,
∵函数g(x)在[0,1]上的上界是T(m),由有界函数的定义可得,
|g(x)|≤T(m)任意x∈[0,1]恒成立,
∴T(m)≥1;
②当m=0时,g(x)=1,|g(x)|=1,
∵函数g(x)在[0,1]上的上界是T(m),由有界函数的定义可得,
|g(x)|≤T(m)任意x∈[0,1]恒成立,
∴T(m)≥1;
③当﹣1<m<0时,x∈[0,1],
∵y=mx2+1在[0,1]上单调递减,
∴g(x)在[0,1]上递增,
∴g(0)≤g(x)≤g(1),即 ![]() ,
,
∴ ![]() ,
,
∵函数g(x)在[0,1]上的上界是T(m),由有界函数的定义可得,
|g(x)|≤T(m)任意x∈[0,1]恒成立,
∴ ![]() .
.
综合①②③,当m≥0时,T(m)的取值范围是[1,+∞),
当﹣1<m<0时,T(m)的取值范围是 ![]()
【解析】(Ⅰ)将a=1代入f(x)可得 ![]() ,利用指数函数的单调性判断出f(x)在(﹣∞,0)上是单调递减函数,即可求得f(x)>f(0),从而得到f(x)的值域,根据有界函数函数的定义,即可判断出f(x)不是有界函数;(Ⅱ)根据有界函数的定义,可得|f(x)|≤3在[0,+∞)上恒成立,利用参变量分离转化为
,利用指数函数的单调性判断出f(x)在(﹣∞,0)上是单调递减函数,即可求得f(x)>f(0),从而得到f(x)的值域,根据有界函数函数的定义,即可判断出f(x)不是有界函数;(Ⅱ)根据有界函数的定义,可得|f(x)|≤3在[0,+∞)上恒成立,利用参变量分离转化为 ![]() 在[0,+∞)上恒成立,令t=2x , 则
在[0,+∞)上恒成立,令t=2x , 则 ![]() ,
, ![]() ,问题转化为求h(t)的最大值和p(t)最小值,利用函数单调性的定义,分别判断出函数h(t)和p(t)的单调性,即可求得最值,从容求得a的取值范围.(Ⅲ)将函数g(x)=
,问题转化为求h(t)的最大值和p(t)最小值,利用函数单调性的定义,分别判断出函数h(t)和p(t)的单调性,即可求得最值,从容求得a的取值范围.(Ⅲ)将函数g(x)= ![]() 变形为g(x)=﹣1+
变形为g(x)=﹣1+ ![]() ,对参数m进行分类讨论,当m>0时,确定函数g(x)的单调性,根据单调性可得g(x)的取值范围,从而确定|g(x)|的范围,利用有界函数的定义,转化为|g(x)|≤T(m)任意x∈[0,1]恒成立,利用所求得的g(x)的范围,即可求得T(m)的取值范围,同理研究当m=0和当﹣1<m<0时的情况,综上所求范围,即可求得T(m)的取值范围.
,对参数m进行分类讨论,当m>0时,确定函数g(x)的单调性,根据单调性可得g(x)的取值范围,从而确定|g(x)|的范围,利用有界函数的定义,转化为|g(x)|≤T(m)任意x∈[0,1]恒成立,利用所求得的g(x)的范围,即可求得T(m)的取值范围,同理研究当m=0和当﹣1<m<0时的情况,综上所求范围,即可求得T(m)的取值范围.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案